LCR-动态规划

2024-11-01 | 阅读：次

1.斐波那契数

斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1

给定 n ，请计算 F(n) 。

答案需要取模 1e9+7(1000000007) ，如计算初始结果为：1000000008，请返回 1。

示例 1：

输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2：

输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2

示例 3：

输入：n = 4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3

提示：

0 <= n <= 100

思路

简单dp

Code

const int MOD = 1e9 + 7;
class Solution {
public:
    int fib(int n) {
        if (n == 0) return 0;
        int f0 = 0, f1 = 1;
        for (int i = 2; i <= n; ++i) {
            int f_new = f0 + f1;
            f_new %= MOD;
            f0 = f1;
            f1 = f_new;
        }
        return f1;
    }
};

2.跳跃训练

今天的有氧运动训练内容是在一个长条形的平台上跳跃。平台有 num 个小格子，每次可以选择跳 一个格子 或者 两个格子。请返回在训练过程中，学员们共有多少种不同的跳跃方式。

结果可能过大，因此结果需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

输入：n = 2
输出：2

示例 2：

输入：n = 5
输出：8

提示：

0 <= n <= 100

思路

跳楼梯，dp 即可。如果开始不能直接写出双变量的代码，可以先写出用数组 dp 的代码，然后再改成双变量。

Code

const int MOD = 1e9 + 7;
class Solution {
public:
    int trainWays(int num) {
        if (num == 1 || num == 0) return 1;
        int f1 = 1, f2 = 2;
        for (int i = 3; i <= num; ++i) {
            int f_new = f1 + f2;
            f_new %= MOD;
            f1 = f2;
            f2 = f_new;
        }
        return f2;
    }
};

3.正则表达式匹配

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素

所谓匹配，是要涵盖整个字符串 s 的，而不是部分字符串。

示例 1：

输入：s = "aa", p = "a"
输出：false
解释："a" 无法匹配 "aa" 整个字符串。

示例 2:

输入：s = "aa", p = "a*"
输出：true
解释：因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

示例 3：

输入：s = "ab", p = ".*"
输出：true
解释：".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

提示：

1 <= s.length <= 20
1 <= p.length <= 20
s 只包含从 a-z 的小写字母。
p 只包含从 a-z 的小写字母，以及字符 . 和 *。
保证每次出现字符 * 时，前面都匹配到有效的字符

思路

设 s 的长度为 n ，p 的长度为 m ；将 s 的第 i 个字符记为 si ，将 p 的第 j 个字符记为 pj ，将 s 的前 i 个字符组成的子字符串记为 s[:i] ，同理将 p 的前 j 个字符组成的子字符串记为 p[:j] 。于是原问题可转化为求 s[:i] 与 p[:j] 能否匹配。

总体思路是从 s[:1] 和 p[:1] 开始判断能否匹配，每轮添加一个字符并判断是否能匹配，直至添加完整个字符串 s 和 p 。我们假设 s[:i] 和 p[:j] 可以匹配，那么下一个状态有两种：

添加一个字符 si+1 后是否能匹配？
添加字符 pj+1 后是否能匹配？

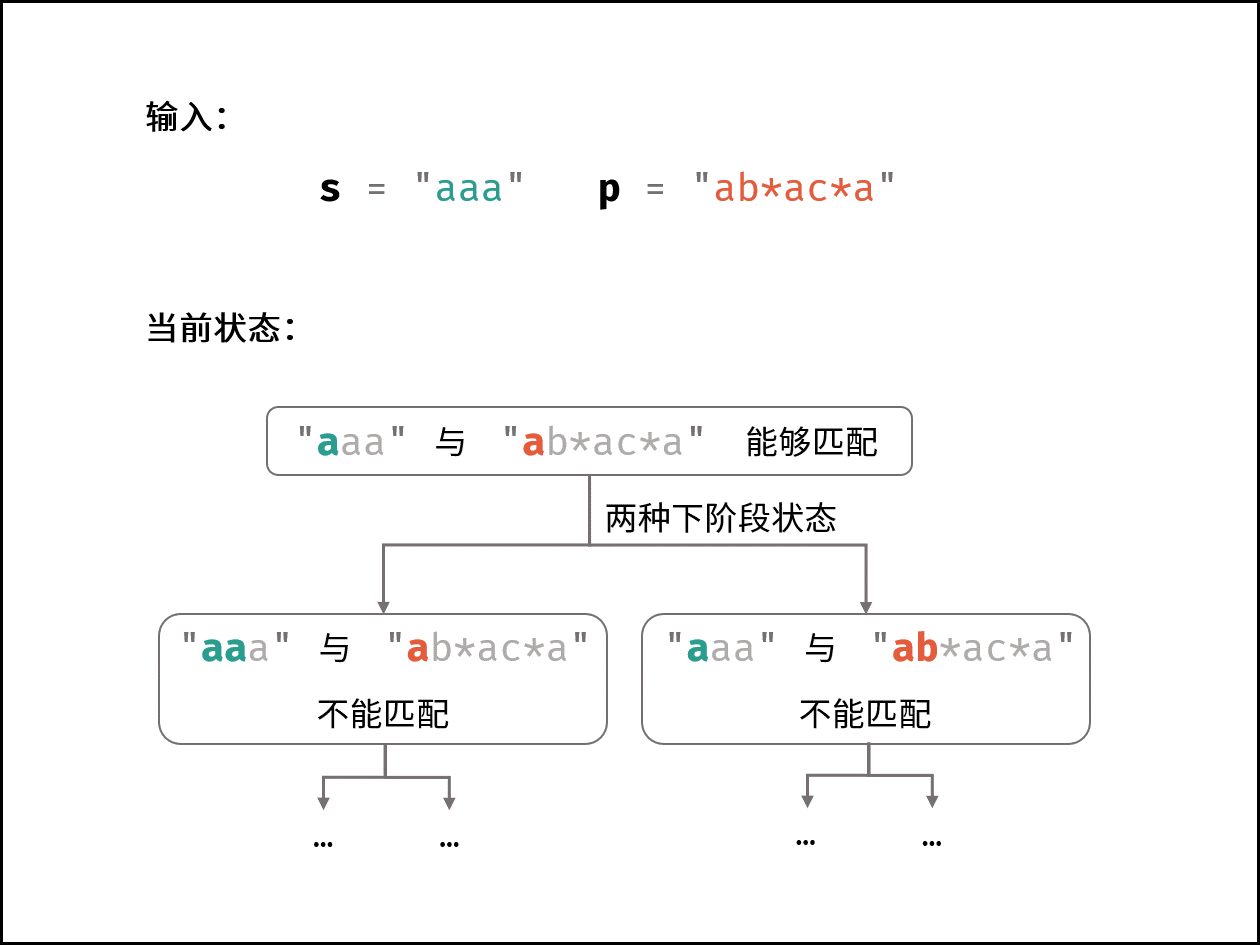
因此，我们有以下状态定义与转移方程：

状态定义：设动态规划矩阵 dp ， dp[i][j] 代表字符串 s 的前 i 个字符和 p 的前 j 个字符能否匹配。
转移方程：需要注意，由于 dp[0][0] 代表的是空字符的状态，因此 dp[i][j] 对应的添加字符是 s[i-1] 和 p[j-1] 。
- 当 p[j-1] == '*' 时，dp[i][j] 在当以下任意情况为 true 时等于 true ：
  1. dp[i][j-2] ：表示在 p[j-1] 之前的字符都能匹配。
  2. dp[i-1][j] 且 s[i-1] = p[j-2]: 即让字符 p[j-2] 多出现 1 次时，能否匹配。
  3. dp[i-1][j] 且 p[j-2] = '.' ：即让字符 '.' 多出现 1 次时，能否匹配。
- 当 p[j-1] != '*' 时，dp[i][j] 在当以下任意情况为 true 时等于 true ：
  1. dp[i-1][j-1] 且 s[i-1] == p[j-1] ：前面能够匹配并且当前字符也相等。
  2. dp[i-1][j-1] 且 p[j-1] == '.' ：前面能够匹配，并且当前位代表任何字符，可以匹配。
初始化：需要先初始化矩阵首行，避免索引越界。
- dp[0][0] = true ：两个空字符串能够匹配。
- dp[0][j] == dp[0][j-2] 且 p[j-1] == '*' ：对于首行， s 此时为空字符串，因此当 p 的偶数位为 * 时才能够匹配（即让 p 的奇数位出现 0 次，保持 p 是空字符串）。因此，循环遍历字符串 p ，步长为 2 （只看偶数位）。

Code

class Solution {
public:
    bool isMatch(string s, string p) {
        int m = s.size() + 1, n = p.size() + 1;
        vector<vector<bool>> dp(m, vector<bool>(n, false));
        dp[0][0] = true;
        for (int j = 2; j < n; j += 2) 
            dp[0][j] = dp[0][j-2] && p[j-1] == '*';
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                dp[i][j] = p[j-1] == '*' ? 
                    dp[i][j-2] || dp[i-1][j] && (s[i-1] == p[j-2] || p[j-2] == '.') : 
                    dp[i-1][j-1] && (p[j-1] == '.' || s[i-1] == p[j-1]);
            }
        }
        return dp[m-1][n-1];
    }
};

总结下来，对于字符串类的线性 dp ，一般可以尝试定义状态为 dp[i][j] 代表字符串 s 的前 i 个字符和 p 的前 j 个字符能否匹配 ，再去尝试寻找状态转移方程。

4.最大连续子数组和

某公司每日销售额记于整数数组 sales，请返回所有连续一或多天销售额总和的最大值。

要求实现时间复杂度为 O(n) 的算法。

示例 1:

输入：sales = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：[4,-1,2,1] 此连续四天的销售总额最高，为 6。

示例 2:

输入：sales = [5,4,-1,7,8]
输出：23
解释：[5,4,-1,7,8] 此连续五天的销售总额最高，为 23。 

提示：

1 <= arr.length <= 10^5
-100 <= arr[i] <= 100

思路

线性 dp ，定义 f[i] 表示以 sales[i] 结尾的最大子数组和，那么针对每个 f[i] ，有两种选择：

将自己加到前面的 f[i-1] 后面
自己重新作为子数组的开头

两者取最大值即可，并在遍历过程中更新答案。

Code

class Solution {
public:
    int maxSales(vector<int>& sales) {
        int n = sales.size();
        vector<int> f(n, 0);
        f[0] = sales[0];
        int res = f[0];
        for (int i = 1; i < n; ++i) {
            f[i] = max(sales[i], f[i-1] + sales[i]);
            res = max(f[i], res);
        }
        return res;
    }
};

5.解密数字

现有一串神秘的密文 ciphertext，经调查，密文的特点和规则如下：

密文由非负整数组成
数字 0-25 分别对应字母 a-z

请根据上述规则将密文 ciphertext 解密为字母，并返回共有多少种解密结果。

示例 1:

输入: ciphertext = 216612
输出: 6
解释: 216612 解密后有 6 种不同的形式，分别是 "cbggbc"，"vggbc"，"vggm"，"cbggm"，"cqgbc" 和 "cqgm" 

提示：

0 <= ciphertext < 2^31

思路

定义 f[i] 表示前 i 个数字一共有多少种翻译方案。

每次只需要考虑后面两位，如果可以共同翻译，那么 f[i] = f[i-1] + f[i-2] ，否则只能将其拼在前面字符的后面，有： f[i] = f[i-1] 。

初始化 f[0] = 1 ，表示 0 个数字有一个翻译方案。

Code

class Solution {
public:
    int crackNumber(int ciphertext) {
        string num = to_string(ciphertext);
        int len = num.length();
        vector<int> f(len + 1);
        f[0] = 1;
        f[1] = 1;
        for (int i = 2; i <= len; ++i) {
            int t = (num[i-2] - '0') * 10 + num[i-1] - '0';
            f[i] = t >= 10 && t <= 25 ? f[i-1] + f[i-2] : f[i-1];
        }
        return f[len];
    }
};

6.珠宝的最高价值

现有一个记作二维矩阵 frame 的珠宝架，其中 frame[i][j] 为该位置珠宝的价值。拿取珠宝的规则为：

只能从架子的左上角开始拿珠宝
每次可以移动到右侧或下侧的相邻位置
到达珠宝架子的右下角时，停止拿取

注意：珠宝的价值都是大于 0 的。除非这个架子上没有任何珠宝，比如 frame = [[0]]。

示例 1:

输入: frame = [[1,3,1],[1,5,1],[4,2,1]]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最高价值的珠宝

提示：

0 < frame.length <= 200
0 < frame[0].length <= 200

思路

简单二维 dp ，对于每个格子，最大值只能来自于它上边的格子或左边的格子，两者取最大值加上当前格子的价值，一直推到右下角即可

dp 数组可以多开一行一列，将边界一起处理。

Code

class Solution {
public:
    int jewelleryValue(vector<vector<int>>& frame) {
        int row = frame.size(), col = frame[0].size();
        vector<vector<int>> f(row + 1, vector<int>(col + 1, 0));
        for (int i = 1; i <= row; ++i) {
            for (int j = 1; j <= col; ++j) {
                f[i][j] = frame[i-1][j-1] + max(f[i-1][j], f[i][j-1]);
            }
        }
        return f[row][col];
    }
};

7.约瑟夫环问题

社团共有 num 位成员参与破冰游戏，编号为 0 ~ num-1。成员们按照编号顺序围绕圆桌而坐。社长抽取一个数字 target，从 0 号成员起开始计数，排在第 target 位的成员离开圆桌，且成员离开后从下一个成员开始计数。请返回游戏结束时最后一位成员的编号。

示例 1：

输入：num = 7, target = 4
输出：1

示例 2：

输入：num = 12, target = 5
输出：0

提示：

1 <= num <= 10^5
1 <= target <= 10^6

思路

著名的约瑟夫环问题。

输入 n、m ，记此约瑟夫环问题为「n,m 问题」，设解（最后留下的数字）为 f[n]，则有：

「n,m 问题」：数字环为：0,1,2,...,n - 1 ，解为 f[n]；
「n−1,m 问题」：数字环为：0,1,2,...,n - 2 ，解为 f[n-1]；

对于「n,m 问题」，首轮删除环中第 m 个数字后，得到一个长度为 n−1 的数字环。由于有可能 m>n ，因此删除的数字为 (m−1)%n ，删除后的数字环从下个数字（即 m%n ）开始，设 t=m%n ，可得数字环：t,t+1,t+2,...,0,1,...,t-3,t-2

删除一轮后的数字环也变成了一个「n−1,m 问题」，观察一下数字编号对应关系：

设「n−1,m 问题」某数字为 x ，则可得递推关系：

换而言之，若已知「n−1,m 问题」的解 f[n−1] ，则可通过以上公式计算得到「n,m 问题」的解 f[n]，即：

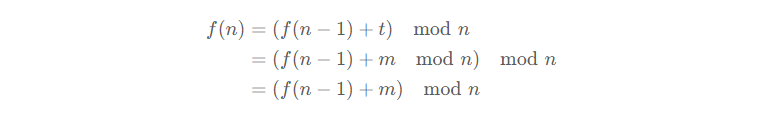
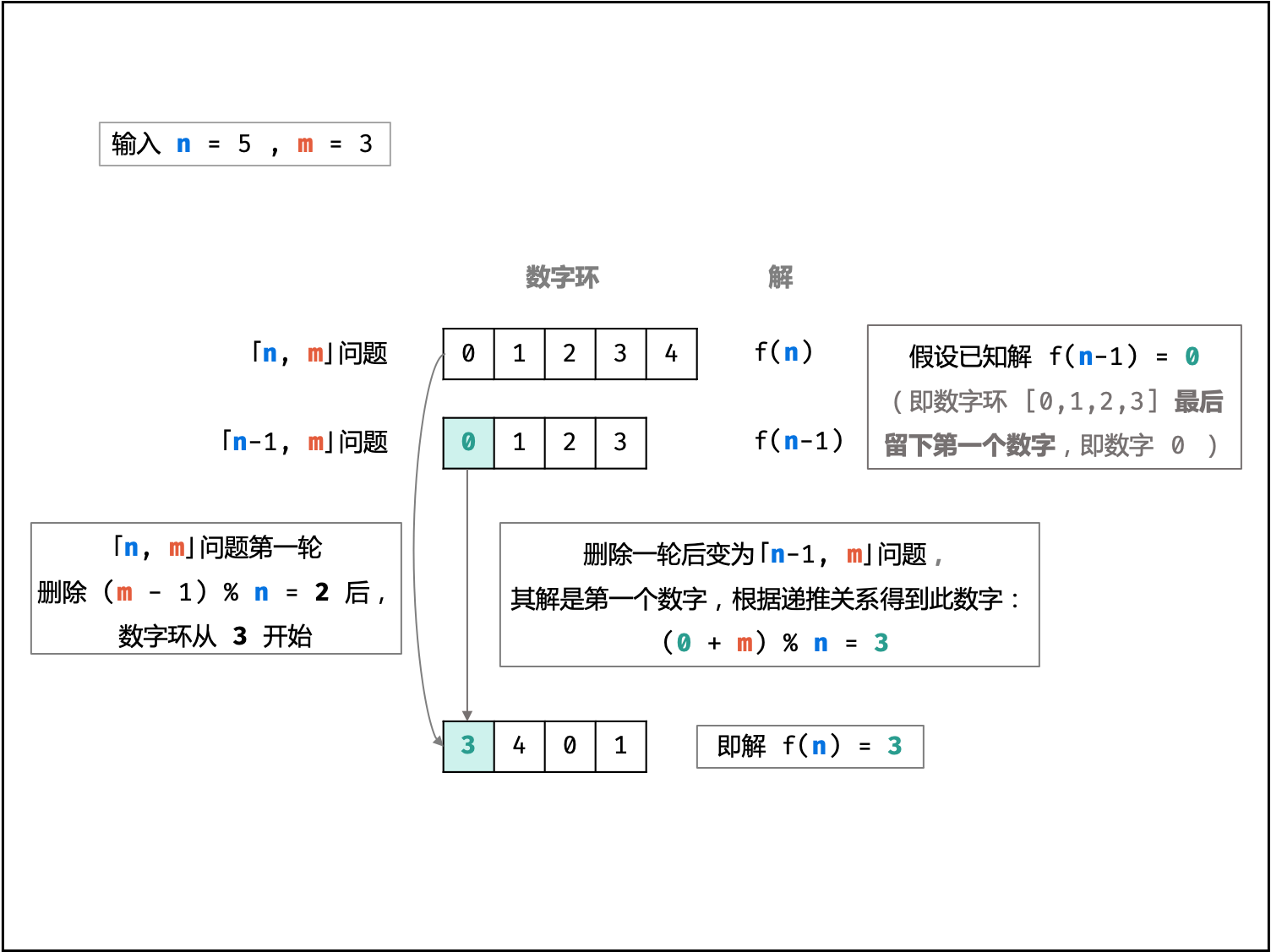
f[n] 可由 f[n-1] 得到，f[n-1] 可由 f[n-2] 得到，……，f[2] 可由 f[1] 得到；因此，若给定 f[1] 的值，就可以递推至任意 f[n] 。而「1,m 问题」的解 f[1]=0 恒成立，即无论 m 为何值，长度为 1 的数字环留下的是一定是数字 0 。

Code

class Solution {
public:
    int iceBreakingGame(int num, int target) {
        int x = 0;
        for (int i = 2; i <= num; ++i) x = (x + target) % i;
        return x;
    }
};

YUKIPEDIA

YUKIPEDIA's blog

LCR-动态规划

目录

1.斐波那契数

2.跳跃训练

3.正则表达式匹配

4.最大连续子数组和

5.解密数字

6.珠宝的最高价值

7.约瑟夫环问题