前言

整理自：https://algo.itcharge.cn/和代码随想录：https://www.programmercarl.com/qita/tulunfabu.html

1.图的基础知识

(1).图的定义

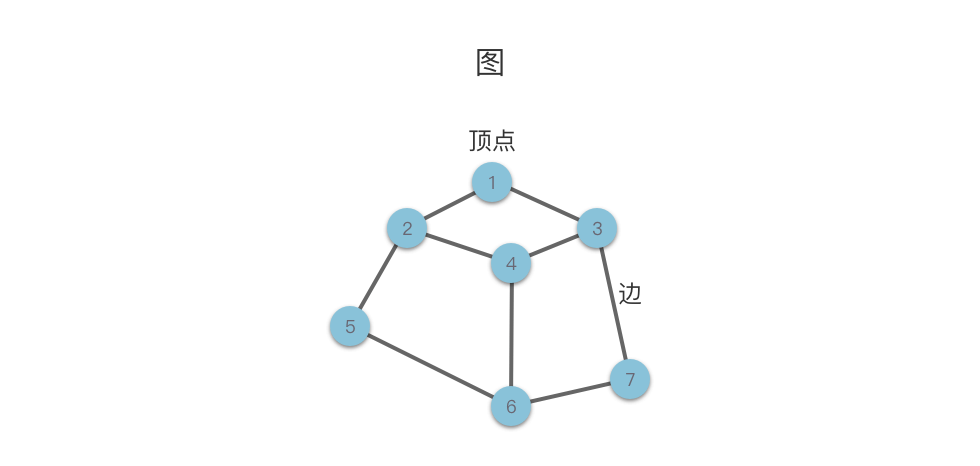
图（Graph）：由顶点的非空有限集合 V （由 n>0 个顶点组成）与边的集合 E（顶点之间的关系）构成的结构。其形式化定义为 G=(V,E)。

• 顶点（Vertex）：图中的数据元素通常称为顶点，在下面的示意图中我们使用圆圈来表示顶点。
• 边（Edge）：图中两个数据元素之间的关联关系通常称为边，在下面的示意图中我们使用连接两个顶点之间的线段来表示边。边的形式化定义为：e=<u,v>，表示从 u 到 v 的一条边，其中 u 称为起始点，v 称为终止点。

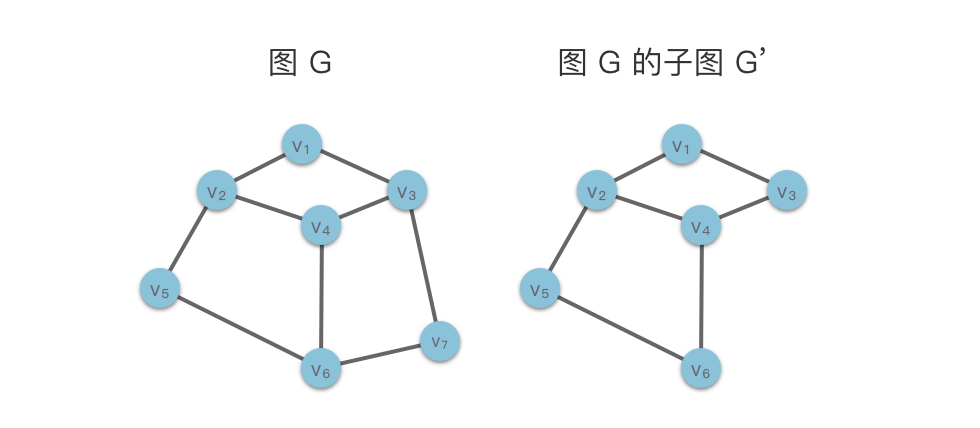
• 子图（Sub Graph）：对于图 G=(V,E) 与 G′=(V′,E′)，如果存在 V′⊆V，E′⊆E，则称图 ′G′ 是图 G 的一个子图。在下面的示意图中我们给出了一个图 G 及其一个子图 G。特别的，根据定义，G 也是其自身的子图。

(2).图的分类

2.1无向图和有向图

按照边是否有方向，我们可以将图分为两种类型：「无向图」和「有向图」。

• 无向图（Undirected Graph）：如果图中的每条边都没有指向性，则称为无向图。例如朋友关系图、路线图都是无向图。
• 有向图（Directed Graph）：如果图中的每条边都具有指向性，则称为有向图。例如流程图是有向图。

如果无向图中有 n 个顶点，则无向图中最多有 n×(n−1)/2 条边。而具有 n×(n−1)/2 条边的无向图称为 「完全无向图（Completed Undirected Graph）」。

如果有向图中有 n 个顶点，则有向图中最多有 n×(n−1) 条弧。而具有 n×(n−1) 条弧的有向图称为 「完全有向图（Completed Directed Graph）」。

2.2环形图和无环图

• 路径：简单来说，如果顶点 vi0 可以通过一系列的顶点和边，到达顶点 vim，则称顶点 vi0 和顶点 vim 之间有一条路径，其中经过的顶点序列则称为两个顶点之间的路径。
• 环（Circle）：如果一条路径的起始点和终止点相同（即 vi0==vim ），则称这条路径为「回路」或者「环」。
• 简单路径：顶点序列中顶点不重复出现的路径称为「简单路径」。

而根据图中是否有环，我们可以将图分为「环形图」和「无环图」。

• 环形图（Circular Graph）：如果图中存在至少一条环路，则该图称为「环形图」。
• 无环图（Acyclic Graph）：如果图中不存在环路，则该图称为「无环图」。

特别的，在有向图中，如果不存在环路，则将该图称为「有向无环图（Directed Acyclic Graph）」，缩写为 DAG。

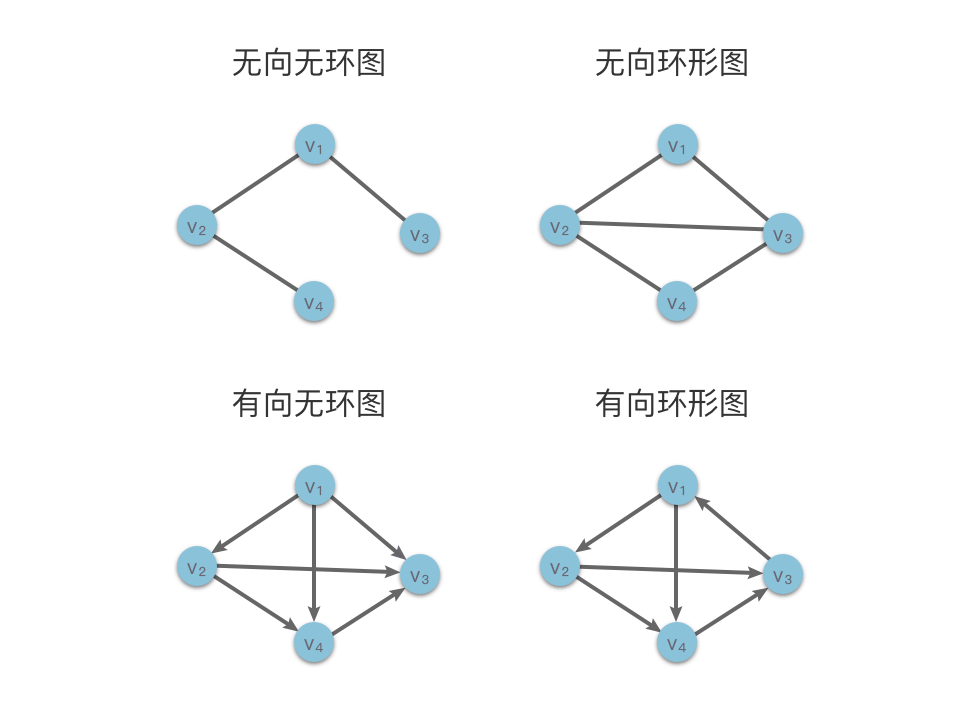
如下图所示，分别为：无向无环图、无向环形图、有向无环图和有向环形图。

2.3连通图和非连通图

2.3.1连通无向图和连通分量

在无向图中，如果从顶点 vi 到顶点 vj 有路径，则称顶点 vi和 vj 是连通的。

• 连通无向图：在无向图中，如果图中任意两个顶点之间都是连通的，则称该图为连通无向图。
• 非连通无向图：在无向图中，如果图中至少存在一对顶点之间不存在任何路径，则该图称为非连通无向图。

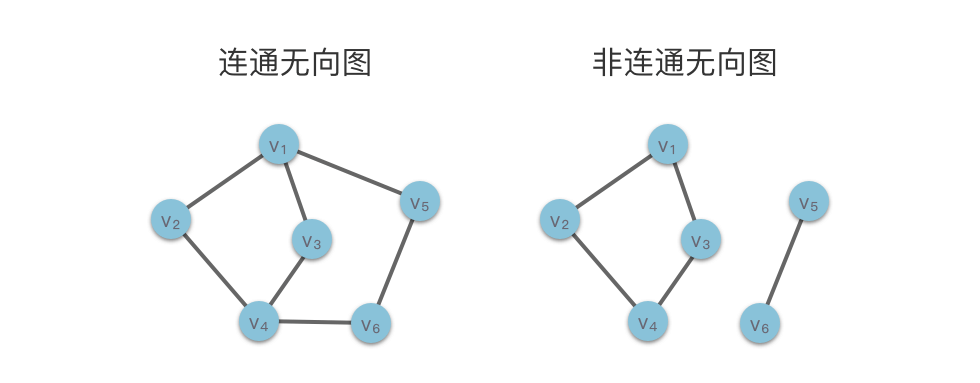
下面介绍一下无向图的「连通分量」概念。有些无向图可能不是连通无向图，但是其子图可能是连通的。这些子图称为原图的连通子图。而无向图的一个极大连通子图（不存在包含它的更大的连通子图）则称为该图的「连通分量」。

• 连通子图：如果无向图的子图是连通无向图，则该子图称为原图的连通子图。
• 连通分量：无向图中的一个极大连通子图（不存在包含它的更大的连通子图）称为该图的连通分量。
• 极大连通子图：无向图中的一个连通子图，并且不存在包含它的更大的连通子图。

比如上图中右边的图是非连通无向图，但是它由 v1、v2、v3、v4 这四个顶点构成的子图是一个连通子图，并且是原图的极大连通子图。所以，这个子图就是原图的一个连通分量。同理，v5、v6 构成的子图也是原图的极大连通子图。

2.3.2强连通有向图和强连通分量

在有向图中，如果从顶点 vi 到 vj 有路径，并且从顶点 vj 到 vi 也有路径，则称顶点 vi 与 vj 是连通的。

• 强连通有向图：如果图中任意两个顶点 vi 和 vj，从 vi 到 vj 和从 vj 到 vi 都有路径，则称该图为强连通有向图。
• 非强连通有向图：如果图中至少存在一对顶点之间不存在任何路径，则该图称为非强连通有向图。

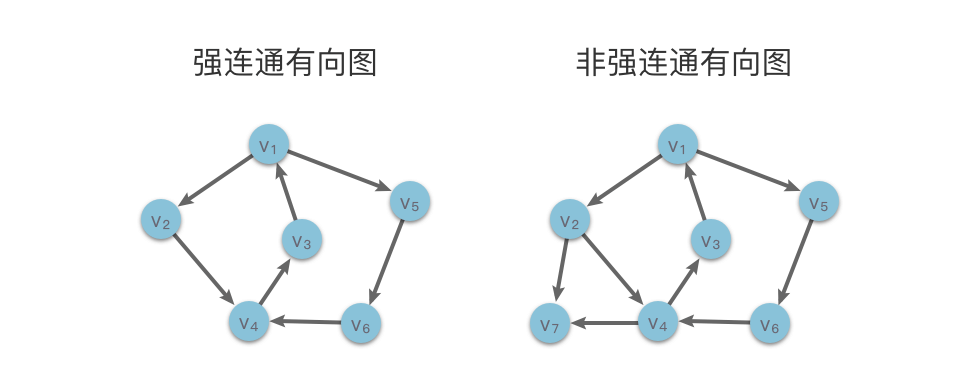
与无向图类似，有向图的一个极大强连通子图称为该图的 强连通分量。

• 强连通子图：如果有向图的子图是连通有向图，则该子图称为原图的强连通子图。
• 强连通分量：有向图中的一个极大强连通子图，称为该图的强连通分量。
• 极大强连通子图：有向图中的一个强连通子图，并且不存在包含它的更大的强连通子图。

如上图所示，左侧的强连通有向图是右侧的非强连通有向图的子图，所以左侧图是右侧图的一个强连通分量。同理，右侧图单独的 v7 也是原图的一个强连通分量

2.4带权图

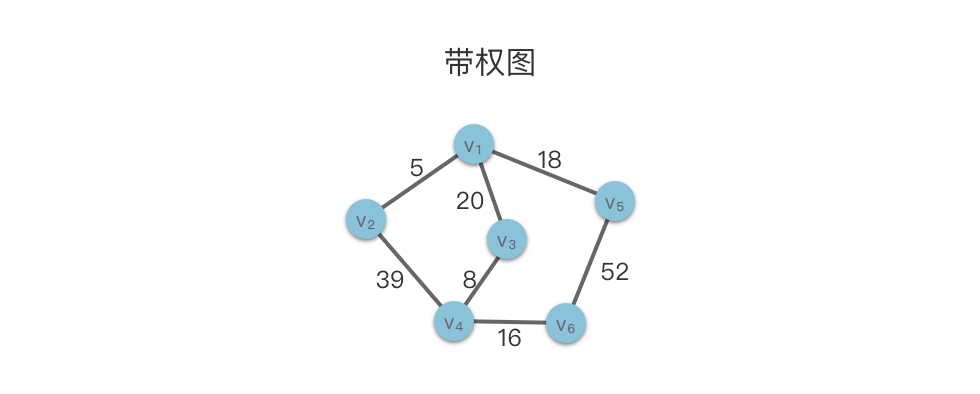
有时，图不仅需要表示顶点之间是否存在某种关系，还需要表示这一关系的具体细节。这时候我们需要在边上带一些数据信息，这些数据信息被称为 权。在具体应用中，权值可以具有某种具体意义，比如权值可以代表距离、时间以及价格等不同属性。

• 带权图：如果图的每条边都被赋以⼀个权值，这种图称为带权图。
• 网络：带权的连通无向图称为网络。

(3)图的存储结构

具体可看原网站：https://algo.itcharge.cn/08.Graph/01.Graph-Basic/02.Graph-Structure/

(4)图论问题应用

常见的图论问题应用大概可以分为以下几类：图的遍历问题、图的连通性问题、图的生成树问题、图的最短路径问题 等等。

4.1图的遍历问题

图的遍历：与树的遍历类似，图的遍历指的是从图的某一个顶点出发，按照某种搜索方式对图中的所有节点都仅访问一次。

图的遍历是求解图的连通性问题、拓扑排序和求关键路径等算法的基础。

根据搜索方式的不同，可以将图的遍历分为「深度优先搜索」和「广度优先搜索」。

• 深度优先搜索：从某一顶点出发，沿着⼀条路径⼀直搜索下去，在⽆法搜索时，回退到刚刚访问过的节点。
• 广度优先搜索：从某个顶点出发，⼀次性访问所有未被访问的邻接点，再依次从这些已访问过的邻接点出发，⼀层⼀层地访问。

4.2图的连通性问题

在无向图中，图的连通性问题主要包括：求无向图的连通分量、求点双连通分量（找割点）、求边双连通分量（找桥）、全局最小割问题 等等。

在有向图中，图的连通性问题主要包括：求有向图的强连通分量、最小点基、最小权点基、2-SAT 问题 等等。

4.3图的生成树问题

图的生成树（Spanning Tree）：如果连通图 G 的一个子图是一棵包含图 G 所有顶点的树，则称该子图为 G 的生成树。生成树是连通图的包含图中的所有顶点的极小连通子图。图的生成树不惟一。从不同的顶点出发进行遍历，可以得到不同的生成树。

图的生成树问题主要包括：最小生成树问题、次小生成树问题 和 有向图的最小树形图问题 等等。

• 无向图的最小生成树：如果连通图 G 是一个带权无向图，则生成树的边也带权，则称该带权图中所有带权生成树中权值总和最小的生成树为最小生成树（也称为最小代价生成树）。
• 无向图的次小生成树：如果连通图 G 是一个带权无向图，生成树 T 是图 G 的一个最小生成树，如果有另一棵生成树 T1，T1≠T，满足不存在树 T′，T′≠T，且 w(T′)<W(T1)，则称 T1 是图 G 的次小生成树。
• 有向图的最小树形图：如果连通图 G 是一个带权有向图，以顶点 vi 为根节点的生成树 T 中，顶点 vi 到任意非 vi 顶点的路径存在且唯一，并且生成树 T 中权值总和最小，则该生成树被称为有向图 G 的最小树形图。

4.4图的最短路径问题

图的最短路径问题：如果用带权图来表示真实的交通、物流或社交网络，则边的权重可能代表交通运输费、距离或者熟悉程度。此时我们会考虑两个不同顶点之间的最短路径有多长，这一类问题统称为最短路径。并且我们称路径上的第一个顶点为源点，最后一个顶点为终点。

按照源点数目的不同，可以将图的最短路径问题分为 单源最短路径问题 和 多源最短路径问题。

• 单源最短路径问题：从一个顶点出发到图中其余各个顶点之间的最短路径问题。
• 多源最短路径问题：图中任意两点之间的最短路径问题。

单源最短路径问题 的求解还是 差分约束系统问题 的基础。

除此之外，在实际应用中，有时候除了需要知道最短路径外，还需要知道次最短路径或者第三最短路径。这样的多条最短路径问题称为 k 最短路径问题。

2.图的最短路径

单源最短路径

1.Dijkstra算法

以下面的题为例：

网络延迟时间

有 n 个网络节点，标记为 1 到 n。

给你一个列表 times，表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。

现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1 。

示例 1：

输入：times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
输出：2

示例 2：

输入：times = [[1,2,1]], n = 2, k = 1
输出：1

示例 3：

输入：times = [[1,2,1]], n = 2, k = 2
输出：-1

提示：

• 1 <= k <= n <= 100
• 1 <= times.length <= 6000
• times[i].length == 3
• 1 <= ui, vi <= n
• ui != vi
• 0 <= wi <= 100
• 所有 (ui, vi) 对都 互不相同（即，不含重复边）

思路

定义 g[i][j] 表示节点 i 到 节点 j 这条边的边权。如果没有 i 到 j 的边，则 g[i][j] = ∞。

定义 dis[i] 表示起点 k 到节点 i 的最短路长度，一开始 dis[k] = 0 ，其余 dis[i] = ∞ 表示尚未计算出。

我们的目标是计算出最终的 dis 数组。

• 首先更新起点 k 到其邻居 y 的最短路，即更新 dis[y] 为 g[k][y]。
• 然后取除了起点 k 以外的 dis[i] 的最小值，假设最小值对应的节点是 3 。此时可以断言：dis[3] 已经是 k 到 3 的最短路长度，不可能有其他 k 到 3 的路径更短。反证法：假设存在更短的路径，那么我们一定会从 k 出发，经过一个点 u ，它的 dis[u] 比 dis[3] 还要小，然后再经过一些边到达 3 ，得到更小的 dis[3] 。但是 dis[3] 已经是最小的了，并且图中没有负数边权，所以 u 是不存在的，矛盾。故原命题成立，此时我们得到了 dis[3] 的最终值。
• 用节点 3 到其邻居 y 的边权 g[3][y] 更新 dis[y] ：如果 dis[3] + g[3][y] < dis[y] ，那么更新 dis[y] 为 dis[3] + g[3][y] ，否则不更新。
• 然后取除了节点 k，3 以外的 dis[i] 的最小值，重复上述过程。
• 有数学归纳法可知，这一做法可以得到每个点的最短路。当所有点的最短路都已确定时，算法结束。

写法一：朴素 Dijkstra （适用于稠密图）

对于本题，在计算最短路时，如果发现当前找到的最小最短路等于 ∞，说明有节点不可达，可以提前结束算法，返回 -1。

如果所有节点都可达，返回 max(dis) 。

代码实现时，节点编号改成从 0 开始

class Solution {
public:
    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        vector<vector<int>> g(n, vector<int>(n, INT_MAX / 2)); // 邻接矩阵
        // 建图
        for (auto& t: times) {
            g[t[0]-1][t[1]-1] = t[2];
        }

        // dis[i] 表示起点 k 到 i 的最短距离
        // done[i] 记录起点到 i 的最短路是否已经确定
        vector<int> dis(n, INT_MAX / 2), done(n);
        dis[k-1] = 0;
        while (true) {
            int x = -1;
            // 取出当前最短的 dis[i] ，继续更新
            for (int i = 0; i < n; ++i) {
                if (!done[i] && (x < 0 || dis[i] < dis[x])) {
                    x = i;
                }
            }
            if (x < 0) { // 所有的最短路都已经确定
                return ranges::max(dis);
            }
            if (dis[x] == INT_MAX / 2) { // 存在不可达节点
                return -1;
            }
            done[x] = true; // 最短路长度已确定
            for (int y = 0; y < n; ++y) {
                // 更新 x 的邻居的最短路
                dis[y] = min(dis[y], dis[x] + g[x][y]);
            }
        }
    }
};

时空复杂度均为 O(n^2) 。

写法二：堆优化 Dijkstra （适用于稀疏图）

寻找最小值的过程可以用一个最小堆来快速完成：

• 一开始把 (dis[k], k) 二元组入堆。
• 当节点 x 首次出堆时，dis[x] 就是写法一中寻找的最小最短路。
• 更新 dis[y] 时，把 (dis[y], y) 二元组入堆。

注意，如果一个节点 x 在出堆前，其最短路长度 dis[x] 被多次更新，那么堆中会有多个重复的 x ，并且包含 x 的二元组中的 dis[x] 是互不相同的（因为我们只在找到更小的最短路时才会把二元组入堆）。

所以写法一中的 done 数组可以省去，取而代之的是用出堆的最短路值（记作 dx ）与当前的 dis[x] 比较，如果 dx > dis[x] 说明 x 之前出堆过，我们已经更新了 x 的邻居的最短路，所以这次就不用更新了，继续外层循环。

class Solution {
public:
    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        vector<vector<pair<int, int>>> g(n); // 邻接表
        // 建图
        for (auto& t: times) {
            g[t[0]-1].emplace_back(t[1] - 1, t[2]);
        }

        vector<int> dis(n, INT_MAX);
        dis[k-1] = 0;
        // 最小堆中存放的是 (dis[i], i)
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;
        pq.emplace(0, k - 1); // (dis[k], k) 入堆
        while (!pq.empty()) {
            auto [dx, x] = pq.top();
            pq.pop();
            // x 之前出堆过
            if (dx > dis[x]) continue;
            for (auto& [y, d] : g[x]) {
                int new_dis = dx + d;
                if (new_dis < dis[y]) {
                    dis[y] = new_dis;
                    pq.emplace(new_dis, y);
                }
            }
        }
        int mx = ranges::max(dis);
        return mx < INT_MAX ? mx : -1;
    }
};

如果输入的是稠密图，写法二的时间复杂度不如写法一

3.DFS 与 BFS 遍历图

DFS 部分

因为 dfs 搜索一直往一个方向深入，并需要回溯，所以用递归方式来实现是最方便的。

dfs 代码框架

void dfs(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本节点所连接的其他节点) {
        处理节点;
        dfs(图，选择的节点); // 递归
        回溯，撤销处理结果
    }
}

BFS 部分

广搜的搜索方式适合解决两个点之间的最短路径问题。

因为广搜是从起点出发，以起始点为中心一圈一圈进行搜索，一旦遇到终点，记录之前走过的节点就是一条最短路。

当然，也有一些问题是广搜和深搜都可以解决的，例如岛屿问题，这类问题的特征就是不涉及具体的遍历方式，只要能把相邻且相同属性的节点标记上就行。

BFS 的实现需要通过队列实现，具体的代码可以看下面的例题。

对于图上的 DFS 和 BFS ，我们均通过下面这道寻找连通分量的题来学习。

省份数量

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

示例 1：

输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

示例 2：

输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

提示：

• 1 <= n <= 200
• n == isConnected.length
• n == isConnected[i].length
• isConnected[i][j] 为 1 或 0
• isConnected[i][i] == 1
• isConnected[i][j] == isConnected[j][i]

一、DFS 解法

题意翻译一下就是：给你一个图的邻接矩阵，要你判断这个图中有多少个连通分量，我们可以通过 DFS 解决。

遍历邻接矩阵中的每个节点，从该节点为起点开始进行 DFS ，直到找不到下一个相邻的节点，就相当于找到了一个连通分量，更新答案。

注意：为了避免重复访问相同的节点，我们需要创建一个 vis 数组记录是否访问过当前节点。

Code

class Solution {
public:
    void dfs(vector<vector<int>>& isConnected, vector<int>& vis, int n, int i) {
        for (int j = 0; j < n; ++j) {
            if (isConnected[i][j] && !vis[j]) {
                vis[j] = 1;
                dfs(isConnected, vis, n, j);
            }
        }
    }

    int findCircleNum(vector<vector<int>>& isConnected) {
        int n = isConnected.size();
        vector<int> vis(n);
        int res = 0;
        for (int i = 0; i < n; ++i) {
            if (!vis[i]) {
                dfs(isConnected, vis, n, i);
                ++res;
            }
        }
        return res;
    }
};

二、BFS 解法

除了使用一路到底的 DFS 搜索图中所有的连通分量，我们还可以使用 BFS 解决这个问题。

实现 BFS 需要用到队列，可以参考下面的模板。

Code

class Solution {
public:
    int findCircleNum(vector<vector<int>>& isConnected) {
        int n = isConnected.size();
        vector<int> vis(n);
        int res = 0;
        queue<int> q;
        for (int i = 0; i < n; ++i) {
            if (!vis[i]) {
                q.push(i);
                while (!q.empty()) {
                    int j = q.front();
                    q.pop();
                    vis[j] = 1;
                    for (int k = 0; k < n; ++k) {
                        if (isConnected[j][k] && !vis[k]) {
                            q.push(k);
                        }
                    }
                }
                ++res;
            }
        }
        return res;
    }
};

4.并查集

并查集原理

并查集通常用来解决连通性问题，当我们需要判断两个元素是否在同一个集合里的时候，我们就要想到用并查集。

并查集主要有两个功能：

• 将两个元素添加到一个集合中
• 判断两个元素在不在同一个集合中

从代码层面，我们如何将两个元素添加到同一个集合中呢？

我们将三个元素A，B，C（分别是数字）放在同一个集合，其实就是将三个元素连通在一起，那么如何连通呢？

只需要用一个一维数组来表示，即：father[A] = B，father[B] = C 。这样就表述 A 与 B 与 C 连通了（有向连通图）。

// 将v，u 这条边加入并查集
void join(int u, int v) {
    u = find(u); // 寻找u的根
    v = find(v); // 寻找v的根
    if (u == v) return; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
    father[v] = u;
}

这里可能会有疑问：这样我可以知道 A 连通 B，因为 A 是索引下标，根据 father[A]的数值就知道 A 连通 B。那怎么知道 B 连通 A呢？

我们的目的是判断这三个元素是否在同一个集合里，知道 A 连通 B 就已经足够了。

这里要讲到寻根思路，只要 A ，B，C 在同一个根下就是同一个集合。

给出 A 元素，就可以通过 father[A] = B，father[B] = C，找到根为 C。

给出 B 元素，就可以通过 father[B] = C，找到根也为为 C，说明 A 和 B 是在同一个集合里。

第一段代码中有一个 find函数 ，这是并查集的寻根函数，其实就是通过数组下标找到数组元素，一层一层寻根：

// 并查集里寻根的过程
int find(int u) {
    if (u == father[u]) return u; // 如果根就是自己，直接返回
    else return find(father[u]); // 如果根不是自己，就根据数组下标一层一层向下找
}

如何表示 C 也在同一个集合里呢？ 我们需要 father[C] = C，即C的根也为C，这样就方便表示 A，B，C 都在同一个集合里了。

所以 father 数组初始化时要 father[i] = i ，默认自己指向自己。

// 并查集初始化
void init() {
    for (int i = 0; i < n; ++i) {
        father[i] = i;
    }
}

最后我们如何判断两个元素是否在同一个集合里？如果通过 find函数 找到两个元素属于同一个根的话，那么这两个元素就是同一个集合。

// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
    u = find(u);
    v = find(v);
    return u == v;
}

路径压缩

在实现 find 函数的过程中，我们知道，通过递归的方式，不断获取father数组下标对应的数值，最终找到这个集合的根。

搜索过程像是一个多叉树中从叶子到根节点的过程，如图：

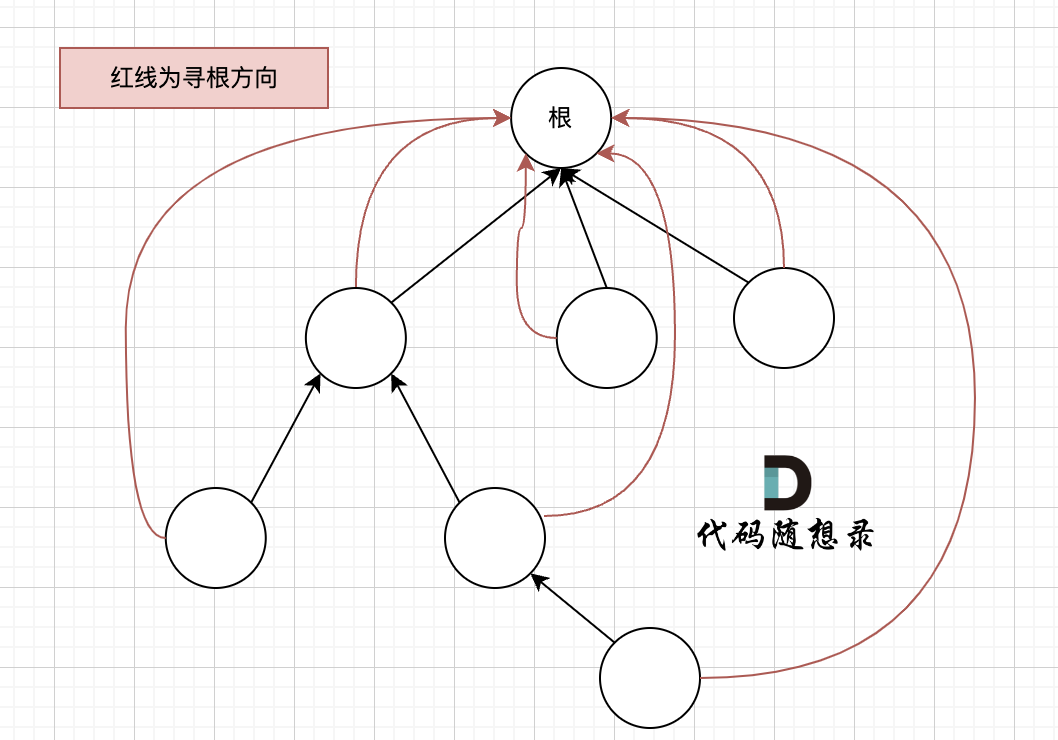
如果这棵多叉树高度很深的话，每次find函数 去寻找根的过程就要递归很多次。

我们的目的只需要知道这些节点在同一个根下就可以，所以对这棵多叉树的构造只需要这样就可以了，如图：

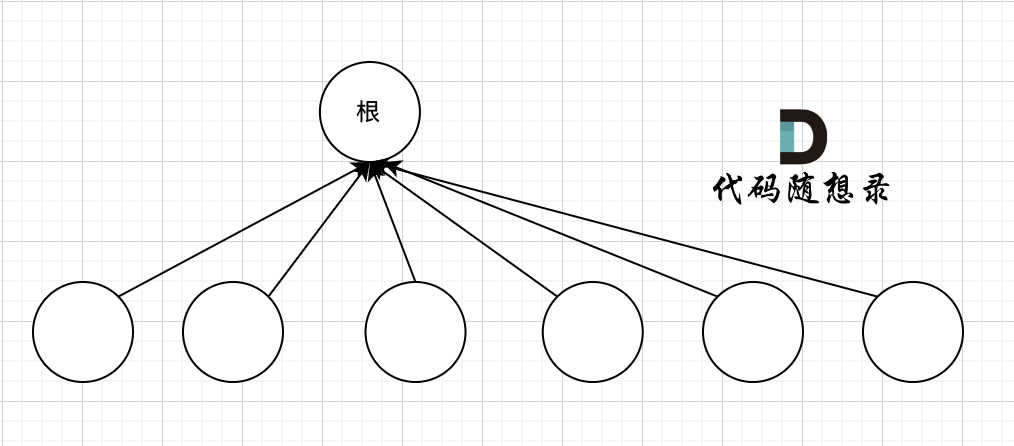
除了根节点其他所有节点都挂载根节点下，这样我们在寻根的时候就很快。

想要达到这样的效果，就需要路径压缩，将非根节点的所有节点直接指向根节点。那么在代码层面如何实现呢？

我们只需要在递归的过程中，让 father[u] 接住 递归函数 find(father[u]) 的返回结果。

因为 find 函数向上寻找根节点，father[u] 表述 u 的父节点，那么让 father[u] 直接获取 find函数 返回的根节点，这样就让节点 u 的父节点变成根节点。

// 并查集里寻根的过程
int find(int u) {
    if (u == father[u]) return u;
    else return father[u] = find(father[u]); // 路径压缩
}

用三目运算符精简一下：

int find(int u) {
	return u == father[u] ? u : father[u] = find(father[u]);
}

并查集模板

int n = 1005; // n根据题目中节点数量而定，一般比节点数量大一点就好
vector<int> father = vector<int> (n, 0); // C++里的一种数组结构

// 并查集初始化
void init() {
    for (int i = 0; i < n; ++i) {
        father[i] = i;
    }
}
// 并查集里寻根的过程
int find(int u) {
    return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}

// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
    u = find(u);
    v = find(v);
    return u == v;
}

// 将v->u 这条边加入并查集
void join(int u, int v) {
    u = find(u); // 寻找u的根
    v = find(v); // 寻找v的根
    if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
    father[v] = u;
}

通过模板，我们可以知道，并查集主要有三个功能：

1. 寻找根节点，函数：find(int u) ，也就是判断这个节点的祖先节点是哪个
2. 将两个节点接入到同一个集合，函数：join(int u, int v) ，将两个节点连在同一个根节点上
3. 判断两个节点是否在同一个集合，函数：isSame(int u, int v) ，就是判断两个节点是不是同一个根节点

例题

1.冗余连接

树可以看成是一个连通且 无环 的 无向 图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的那个。

示例 1：

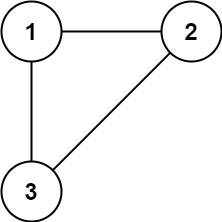
输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]

示例 2：

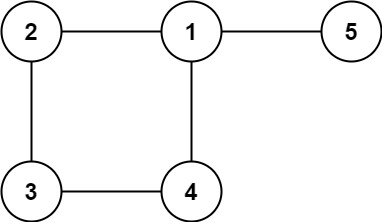
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]

提示:

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ai < bi <= edges.length
• ai != bi
• edges 中无重复元素
• 给定的图是连通的

思路

一棵树中边的数量比节点数量少 1。如果一棵树有 n 个节点，则这棵树有 n - 1 条边。

树是一个连通且无环的无向图，在树中多了一条附加的边之后就会出现环，因此附加的边即为导致环出现的边。

可以通过并查集寻找附加的边。初始时，每个节点都属于不同的连通分量。遍历每一条边，判断这条边连接的两个顶点是否属于相同的连通分量。

• 如果两个顶点属于不同的连通分量，则说明在遍历到当前的边之前，这两个顶点之间不连通，因此当前的边不会导致环的出现，合并这两个顶点的连通分量。
• 如果两个顶点属于相同的连通分量，则说明在遍历到当前的边之前，这两个顶点之间已经连通，因此当前的边导致环出现，为附加的边，将当前的边作为答案返回。

Code

class Solution {
private:
    int n = 1005; // n根据题目中节点数量而定，一般比节点数量大一点就好
    vector<int> father = vector<int> (n, 0); // C++里的一种数组结构

    // 并查集初始化
    void init() {
        for (int i = 0; i < n; ++i) {
            father[i] = i;
        }
    }
    // 并查集里寻根的过程
    int find(int u) {
        return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
    }

    // 判断 u 和 v是否找到同一个根
    bool isSame(int u, int v) {
        u = find(u);
        v = find(v);
        return u == v;
    }

    // 将v->u 这条边加入并查集
    void join(int u, int v) {
        u = find(u); // 寻找u的根
        v = find(v); // 寻找v的根
        if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
        father[v] = u;
    }

public:
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        init(); // 并查集初始化
        for (auto& edge: edges) { // 遍历每条边
            int node1 = edge[0], node2 = edge[1];
            if (find(node1) != find(node2)) { // 如果不在同一个连通分量，说明这个边没有导致环的出现，合并
                join(node1, node2);
            } else { // 已经在同一个连通分量里，说明当前边导致了环的出现，当前边就是我们要找的边
                return edge;
            }
        }
        return {};
    }
};

2.新增道路查询后的最短距离Ⅱ

给你一个整数 n 和一个二维整数数组 queries。

有 n 个城市，编号从 0 到 n - 1。初始时，每个城市 i 都有一条单向道路通往城市 i + 1（ 0 <= i < n - 1）。

queries[i] = [ui, vi] 表示新建一条从城市 ui 到城市 vi 的单向道路。每次查询后，你需要找到从城市 0 到城市 n - 1 的最短路径的长度。

所有查询中不会存在两个查询都满足 queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]。

返回一个数组 answer，对于范围 [0, queries.length - 1] 中的每个 i，answer[i] 是处理完前 i + 1 个查询后，从城市 0 到城市 n - 1 的最短路径的长度。

示例 1：

输入： n = 5, queries = [[2, 4], [0, 2], [0, 4]]

输出： [3, 2, 1]

解释：

新增一条从 2 到 4 的道路后，从 0 到 4 的最短路径长度为 3。

新增一条从 0 到 2 的道路后，从 0 到 4 的最短路径长度为 2。

新增一条从 0 到 4 的道路后，从 0 到 4 的最短路径长度为 1。

示例 2：

输入： n = 4, queries = [[0, 3], [0, 2]]

输出： [1, 1]

解释：

新增一条从 0 到 3 的道路后，从 0 到 3 的最短路径长度为 1。

新增一条从 0 到 2 的道路后，从 0 到 3 的最短路径长度仍为 1。

提示:

• 3 <= n <= 10^5
• 1 <= queries.length <= 10^5
• queries[i].length == 2
• 0 <= queries[i][0] < queries[i][1] < n
• 1 < queries[i][1] - queries[i][0]
• 查询中不存在重复的道路。
• 不存在两个查询都满足 i != j 且 queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]。

思路

本题满足一个性质：所有查询中不会存在两个查询都满足 queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]。

这说明所有添加的边都不会交叉，从贪心的角度来看，遇到捷径就走捷径是最优的。

考虑如上性质，我们把目光放在边上：

初始有 n - 1 条边，我们在 0 -> 1 这条边上，目标是到达 (n - 2) -> (n - 1) 这条边，并把这条边走完。

处理 queries 之前，我们需要走 n - 1 条边。

连一条 2 到 4 的边，意味着什么？

相当于把 2 -> 3 这条边和 3 -> 4 这条边合并成一条边。现在从起点到终点需要 3 条边。

连一条从 0 到 2 的边，相当于把 0 -> 1 这条边和 1 -> 2 这条边合并成一条边。现在从起点到终点需要 2 条边。

我们可以用并查集实现边的合并。初始化一个大小为 n - 1 的并查集，并查集中的节点 i 表示题目的边 i -> (i + 1) ，这就相当于给每条边编号 0, 1, 2, ..., n - 2 。

连一条从 L 到 R 的边，相当于把并查集中的节点 L, L + 1, L + 2, ... , R - 2 合并到并查集中的节点 R - 1 上。

合并的同时，维护并查集连通块个数，答案就是每次合并后的并查集连通块个数。

Code

class Solution {
public:
    vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) {
        vector<int> fa(n - 1);
        iota(fa.begin(), fa.end(), 0);

        auto find = [&](int x) -> int {
            int rt = x;
            while (fa[rt] != rt) {
                rt = fa[rt];
            }
            while (fa[x] != rt) {
                int tmp = fa[x];
                fa[x] = rt;
                x = tmp;
            }
            return rt;
        };

        vector<int> ans(queries.size());
        int cnt = n - 1;
        for (int qi = 0; qi < queries.size(); ++qi) {
            int l = queries[qi][0], r = queries[qi][1] - 1;
            int fr = find(r);
            for (int i = find(l); i < r; i = find(i + 1)) {
                fa[i] = fr;
                cnt--;
            }
            ans[qi] = cnt;
        }
        return ans;
    }
};

下面分析上面的代码是如何使用并查集的：

• 寻根过程：

while (fa[rt] != rt) {
    rt = fa[rt];
}

逐层跳跃父节点，找到 x 所在连通块的根节点 rt

• 路径压缩：

while (fa[x] != rt) {
    int tmp = fa[x];
    fa[x] = rt;
    x = tmp;
}

优化并查集的结构，将路径上所有节点直接指向根节点 rt ，使树更加“扁平化”。下次查询时，路径上的节点直接指向根节点，大幅加快后续操作的效率。

为什么使用两次循环而不是递归来实现并查集的寻根过程和路径压缩过程？

• 使用迭代而非递归可以避免函数调用栈的额外开销，在深度较大的树上更安全。