LCR-位运算

2024-10-22 | 阅读：次

1.位1的个数

编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为汉明重量).）。

提示：

请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在上面的 示例 3 中，输入表示有符号整数 -3。

示例 1：

输入：n = 11 (控制台输入 00000000000000000000000000001011)
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 '1'。

示例 2：

输入：n = 128 (控制台输入 00000000000000000000000010000000)
输出：1
解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 '1'。

示例 3：

输入：n = 4294967293 (控制台输入 11111111111111111111111111111101，部分语言中 n = -3）
输出：31
解释：输入的二进制串 11111111111111111111111111111101 中，共有 31 位为 '1'。

提示：

输入必须是长度为 32 的 二进制串 。

方法一：逐位判断

由于要求给定无符号整数的二进制 1 的个数，这里可以直接对 2 取模，拿到当前整数 n 的二进制最右边的数字，判断是否为 1 ，然后将 n 右移 1 位，逐位判断即可。

Code

class Solution {
public:
    int hammingWeight(uint32_t n) {
        int res = 0;
        while (n) {
            res += n % 2;
            n >>= 1;
        }
        return res;
    }
};

拿到二进制最右一位也可以通过位运算得到：

若 n & 1 == 0 ，则 n 二进制最右一位为 0；
若 n & 1 == 1 ，则 n 二进制最右一位为 1。

Code

class Solution {
public:
    int hammingWeight(uint32_t n) {
        int res = 0;
        while (n) {
            res += n & 1;
            n >>= 1;
        }
        return res;
    }
};

方法二：巧用 n & (n - 1)

(n - 1) 解析：二进制数字 n 最右边的 1 变成 0，此 1 右边的 0 都变成 1；
n & (n - 1) ：解析：二进制数字 n 最右边的 1 变成 0，其余不变。

当 n 的二进制中还存在 1 时，不停的将 n 与 (n - 1) 做与运算，每一轮能够消除掉 n 中的一个 1，而不用遍历整个 n 的二进制串。

Code

class Solution {
public:
    int hammingWeight(uint32_t n) {
        int res = 0;
        while (n) {
            ++res;
            n &= n - 1;
        }
        return res;
    }
};

2.Pow(x, n)

实现 pow(x, n) ，即计算 x 的 n 次幂函数（即，xn）。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：

输入：x = 2.10000, n = 3
输出：9.26100

示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

提示：

-100.0 < x < 100.0
-2^31 <= n <= 2^31-1
-10^4 <= xn <= 10^4

思路

快速幂算法：快速幂

Code

class Solution {
public:
    double myPow(double x, int N) {
        double ans = 1;
        long long n = N;
        // 处理负数次幂的情况
        if (n < 0) { // x^-n = (1/x)^n
            n = -n;
            x = 1 / x;
        }
        while (n) { // 从低到高枚举 n 的每个比特位
            if (n & 1) { // 当前比特位是 1
                ans *= x; // 把 x 乘到 ans 中
            }
            x *= x; // x 自身平方
            n >>= 1; // n 右移，继续枚举下一个比特位
        }
        return ans;
    }
};

3.撞色搭配

整数数组 sockets 记录了一个袜子礼盒的颜色分布情况，其中 sockets[i] 表示该袜子的颜色编号。礼盒中除了一款撞色搭配的袜子，每种颜色的袜子均有两只。请设计一个程序，在时间复杂度 O(n)，空间复杂度O(1) 内找到这双撞色搭配袜子的两个颜色编号。

示例 1：

输入：sockets = [4, 5, 2, 4, 6, 6]
输出：[2,5] 或 [5,2]

示例 2：

输入：sockets = [1, 2, 4, 1, 4, 3, 12, 3]
输出：[2,12] 或 [12,2]

提示：

2 <= sockets.length <= 10000

思路

翻译题面：给定一个数组，该数组中有两个元素只出现了一次，其他元素均出现了两次。请设计时间复杂度 O(n)，空间复杂度O(1)的算法找到这两个元素。

我们首先考虑一个更简单的问题：给定一个数组，该数组中有一个元素只出现了一次，其他元素均出现了两次，请设计时间复杂度 O(n)，空间复杂度O(1)的算法找到这个元素。

当需要在重复出现的数字数组中找到没有重复出现的数字时，我们可以使用位运算中的异或运算来解决。

异或运算有个重要的性质：

两个相同数字异或，结果为 0；
所有整数和 0 异或，结果为自身。

对于上面的问题，我们可以对所有的数组元素进行异或操作，假设 sockets = [a,a,b,b,...,x] 那么就有：

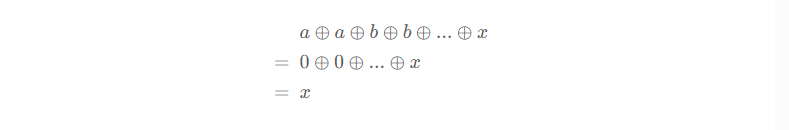
因为异或运算满足交换律，所以以上运算结果与 sockets 的元素顺序无关。

vector<int> singleNumber(vector<int>& sockets) {
    int x = 0;
    for(int num : sockets)  // 1. 遍历 sockets 执行异或运算
        x ^= num;
    return x;            // 2. 返回出现一次的数字 x
}

那么回到原来的问题，我们现在要找的不是一个只出现一次的数字，而是两个只出现一次的数字，如何解决呢？

设两个只出现一次的数字为 x，y ，由于 x != y ，则 x 和 y 的二进制至少有一位不同，根据此位可以将 sockets 拆分为分别包含 x 和 y 的两个子数组。然后分别对两个子数组遍历执行异或操作，就可以得到答案。

算法流程：

遍历 sockets 执行异或：对 sockets 中所有数字执行异或，得到的结果为 x ^ y
循环左移计算 m ：
- 根据异或运算定义，若 x ^ y 的某二进制位为 1，则 x 和 y 的此二进制位一定不同。当我们找到 x ^ y 某个为 1 的二进制位，即可将 sockets 拆分为上述的两个子数组。根据与运算特点，可知对于任意整数 a 有：
  - 若 a & 0001 != 0 ，则 a 的第一位为 1；
  - 若 a & 0010 != 0 ，则 a 的第二位为 1；
  - 以此类推…
- 因此，初始化一个辅助变量 m = 1 ，通过与运算从右往左循环判断，便可获取整数 x ^ y 首位 1，记录在 m 中。
拆分 sockets 为两个子数组
分别遍历两个子数组执行异或，返回两个子数组异或的结果即可

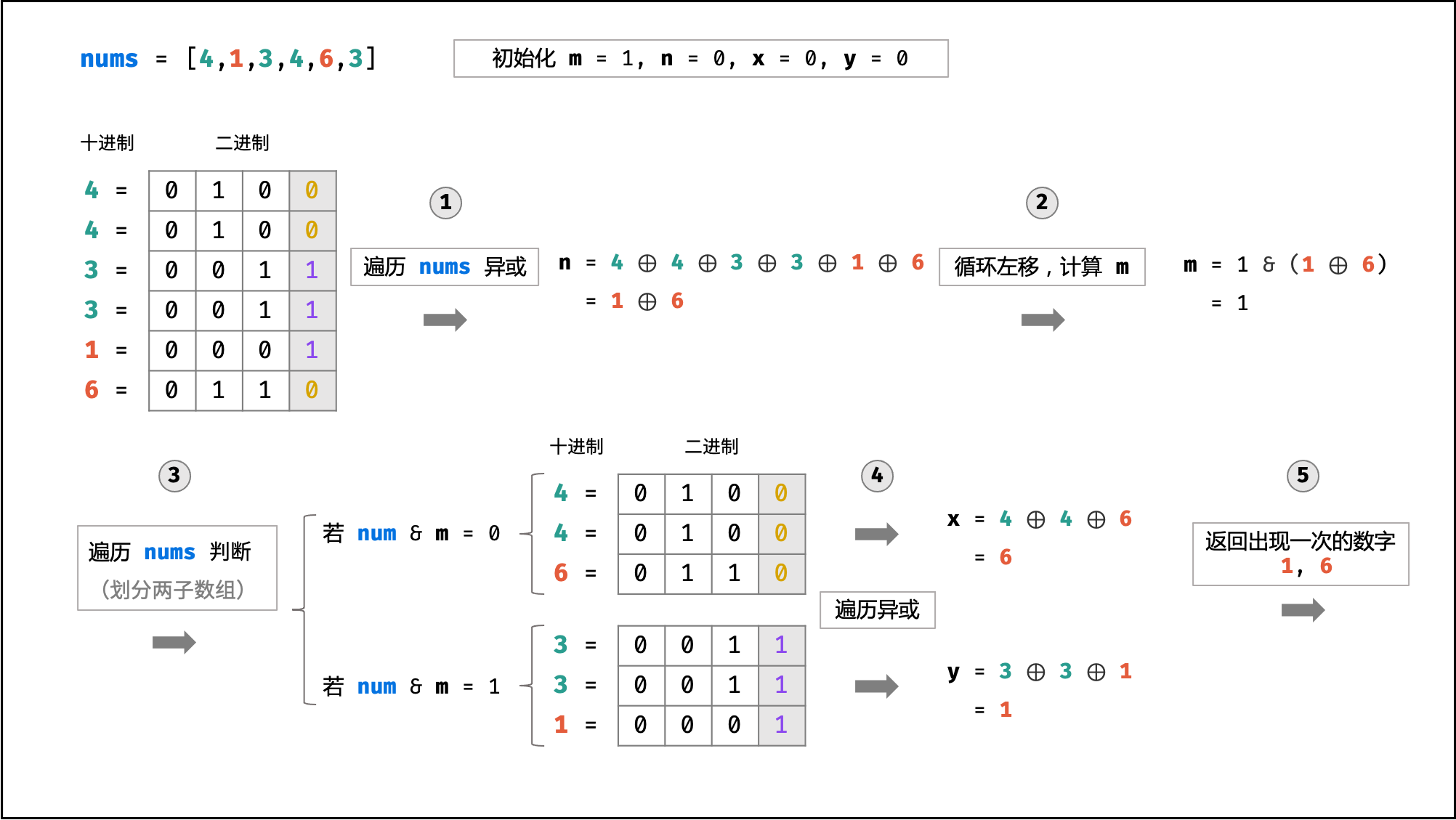
以下面的例子来解释为什么分组：

例子： 1 4 6 4 如果全员异或，相同的4肯定没了，留下1 和 6异或的结果，但是光异或我没法返回啊
	  那这里进行一下分组
      1 和 6 肯定是不同的吧，异或结果有一位肯定是 1，比如说第2位异或为1
                  => 也就是说 1 和 6 ，第二位一个为1一个为0
      那么我就分组，将第二位为1的分一组，全员异或
                  将第二位为0的分一组，全员异或
      这就是最终结果了
      你可能还有疑问，哪相同的元素怎么办，不会干扰结果吗？
         当然不会，比如4 和 4，第二位都为0，肯定都被分到一组，最后异或为0，不影响结果

Code

class Solution {
public:
    vector<int> sockCollocation(vector<int>& sockets) {
        int x = 0, y = 0, n = 0, m = 1;
        for (int num: sockets) n ^= num; // 1.遍历异或
        while ((n & m) == 0) m <<= 1;   // 2.循环左移，计算 m
        for (int num: sockets) {        // 3.遍历 sockets 分组
            if (num & m) x ^= num;      // 4.当 num & m != 0
            else y ^= num;              // 4.当 num & m == 0
        }
        return {x, y};
    }
};

4.训练计划Ⅵ

教学过程中，教练示范一次，学员跟做三次。该过程被混乱剪辑后，记录于数组 actions，其中 actions[i] 表示做出该动作的人员编号。请返回教练的编号。

示例 1：

输入：actions = [5, 7, 5, 5]
输出：7

示例 2：

输入：actions = [12, 1, 6, 12, 6, 12, 6]
输出：1

提示：

1 <= actions.length <= 10000
1 <= actions[i] < 2^31

思路

考虑数字的二进制形式，对于出现三次的数字，各二进制位的出现次数都是 3 的倍数。

因此，统计所有数字的各二进制位中 1 的出现次数，并对 3 求余，结果则为只出现一次的数字。

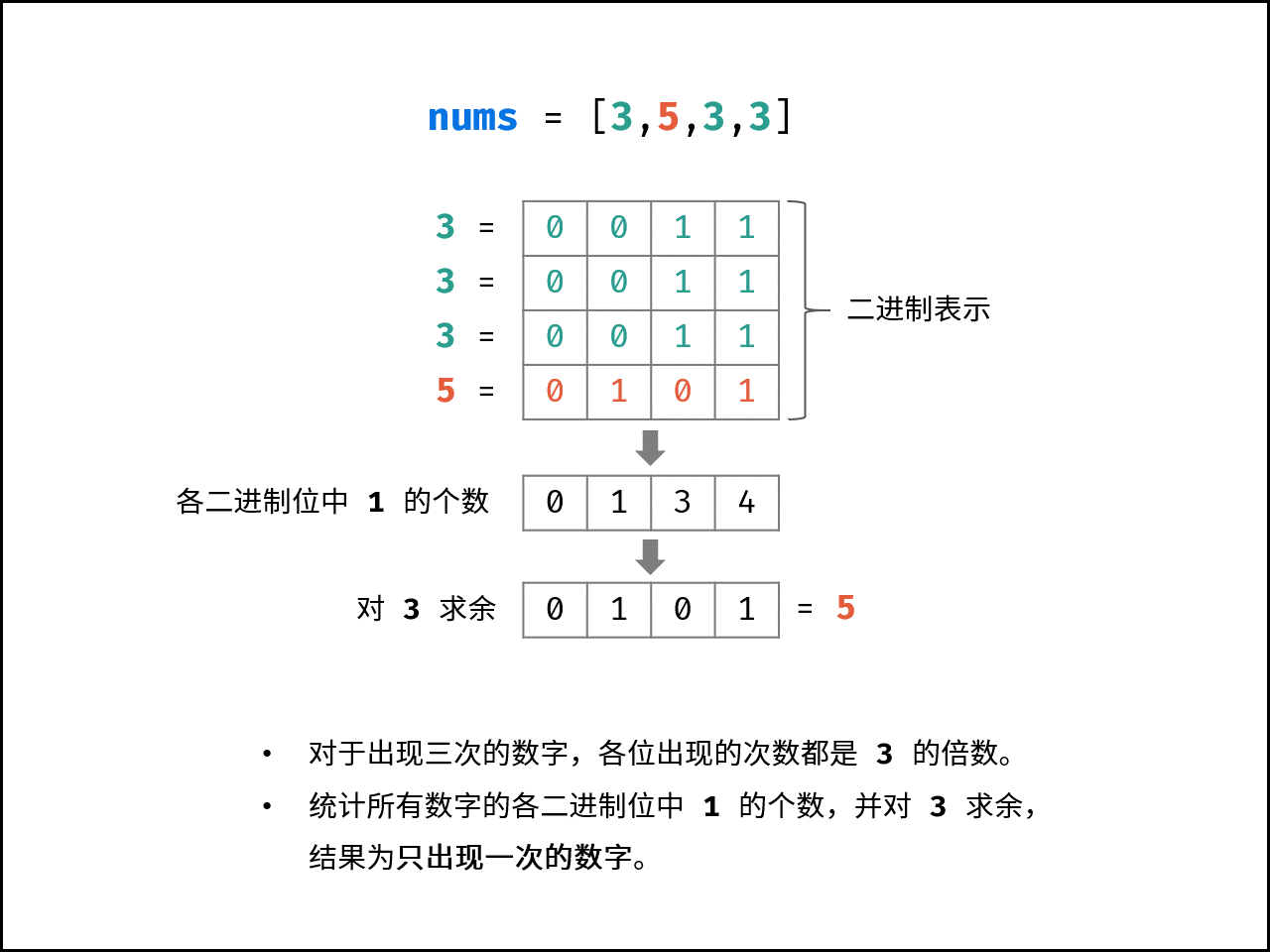
因此，我们可以根据上面的思路进行遍历统计：

使用与运算，可获取二进制数字 action 的最右一位 n1 ：n1 = action & i
配合右移操作，可从低位到高位，获取 action 所有位的值：action = action >> 1

于是我们可以建立一个长度为 32 的数组 counts ，

通过以上方法记录所有数字的各二进制位的 1 的出现次数之和；
将 counts 各元素对 3 求余，则结果为只出现一次的数字的各二进制位。

之后我们要做的就是通过这个 counts 数组恢复出结果 res：

通过左移操作和或运算，可以将各二进制位的值恢复到数字 res 上。

Code

class Solution {
public:
    int trainingPlan(vector<int>& actions) {
        int counts[32] = {0};
        for (int action: actions) {
            for (int i = 0; i < 32; ++i) {
                counts[i] += action & 1;
                action >>= 1;
            }
        }
        int res = 0, m = 3;
        for (int i = 31; i >= 0; --i) {
            res <<= 1;
            res |= counts[i] % m;
        }
        return res;
    }
};

5.加密运算

计算机安全专家正在开发一款高度安全的加密通信软件，需要在进行数据传输时对数据进行加密和解密操作。假定 dataA 和 dataB 分别为随机抽样的两次通信的数据量：

正数为发送量
负数为接受量
0 为数据遗失

请不使用四则运算符的情况下实现一个函数计算两次通信的数据量之和（三种情况均需被统计），以确保在数据传输过程中的高安全性和保密性。

示例 1:

输入：dataA = 5, dataB = -1
输出：4

提示：

dataA 和 dataB 均可能是负数或 0
结果不会溢出 32 位整数

思路

本题需要用位运算实现加法操作。

设两数字的二进制形式 dataA、dataB，其求和 s = dataA + dataB ，dataA(i) 代表 dataA 的二进制第 i 位，则分为以下四种情况：

dataA(i)	dataB(i)	无进位和 n(i)	进位 c(i+1)
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

可以发现，无进位和与异或运算规律相同，进位和与运算规律相同（并需要左移一位）。

同时，有：（和 s ）=（非进位和 n ）+（进位 c ）。

循环求 n 和 c ，直至进位 c = 0；此时 s = n ，返回 n 即可。

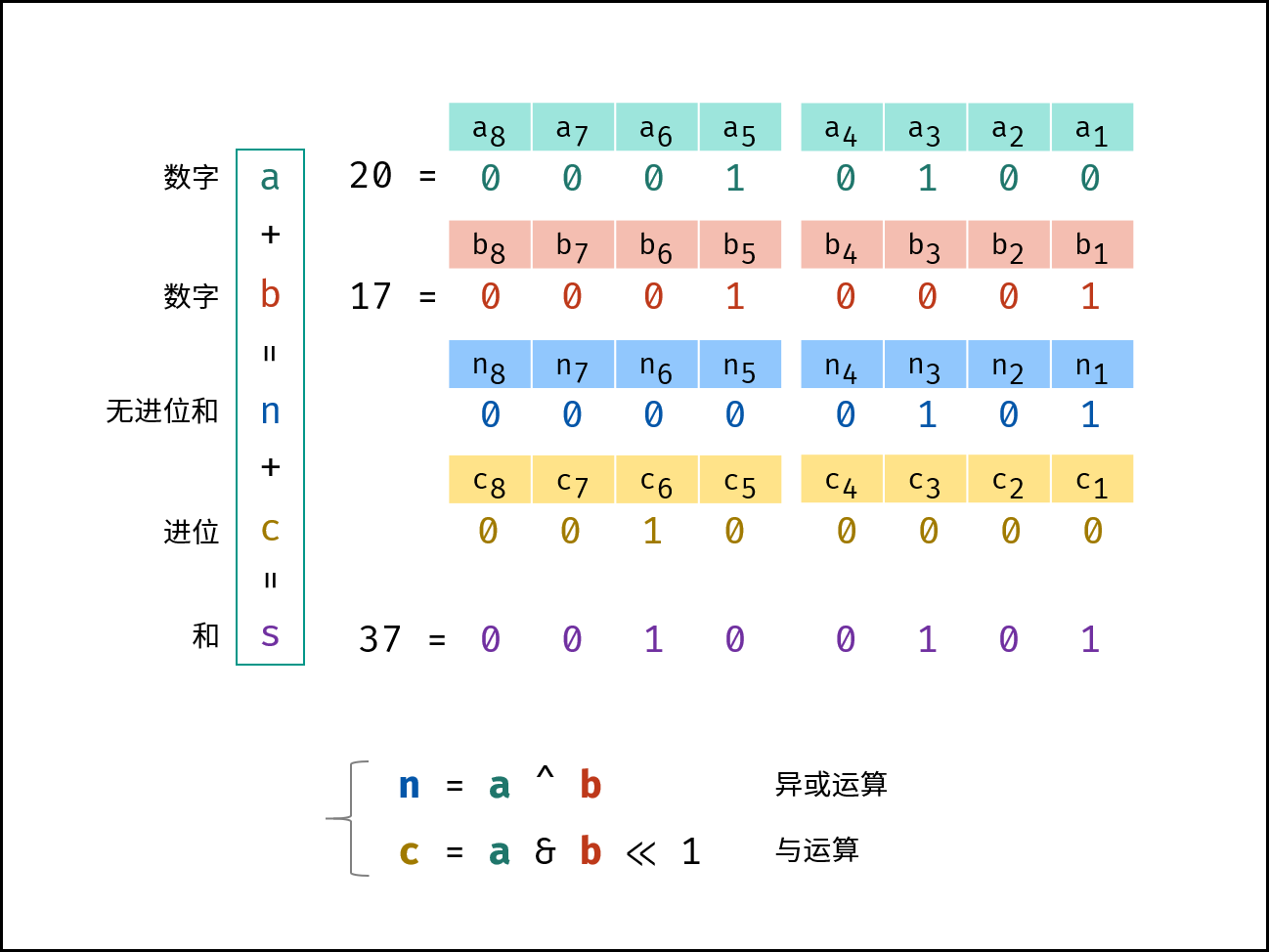
注：负数在计算机系统中用补码表示，加减法可以和正数一样统一处理，因此以上方法适用于正数和负数的加法。

Code

class Solution {
public:
    int encryptionCalculate(int dataA, int dataB) {
        while (dataB != 0) {
            // 进位不存在负的情况，unsigned int 是修饰进位
            int c = (unsigned int) (dataA & dataB) << 1;
            dataA ^= dataB;
            dataB = c;
        }
        return dataA;
    }
};

YUKIPEDIA

YUKIPEDIA's blog

LCR-位运算

目录

1.位1的个数

2.Pow(x, n)

3.撞色搭配

4.训练计划Ⅵ

5.加密运算