LCR-二叉树

2024-10-21 | 阅读：次

1.根据前序与中序遍历序列构造二叉树
2.相同的树
3.对称二叉树
4.平衡二叉树
5.二叉树的右视图
6.子结构判断
7.翻转二叉树（二叉树的镜像）
8.从上到下逐层打印二叉树Ⅰ
9.从上到下逐层打印二叉树Ⅱ
10.从上到下逐层打印二叉树Ⅲ
11.验证二叉搜索树的后序遍历序列
12.二叉树中和为目标值的路径
13.将二叉搜索树转化为排序的双向链表
14.序列化与反序列化二叉树
15.寻找二叉搜索树中的目标节点
16.计算二叉树的深度
17.判断是否为平衡二叉树
18.二叉搜索树的最近公共祖先
19.二叉树的最近公共祖先

1.根据前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

思路

前序遍历：按照「根-左子树-右子树」的顺序遍历二叉树。

中序遍历：按照「左子树-根-右子树」的顺序遍历二叉树。

我们来看看示例 1 是怎么生成这棵二叉树的。

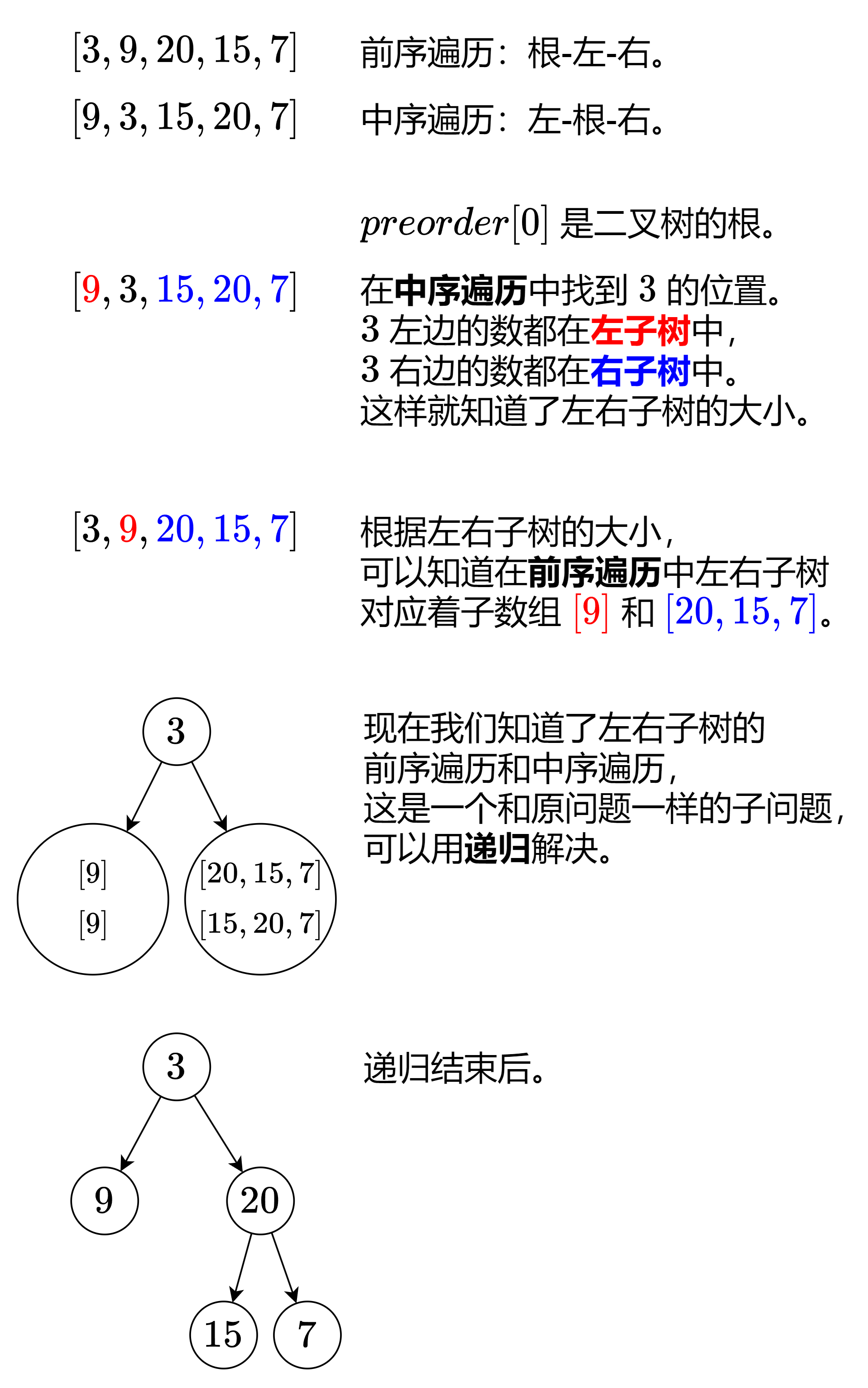
递归边界：如果 preorder 的长度是 0，对应着空节点，返回空。

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if (preorder.empty()) return nullptr; // 空节点

        // 在中序序列中找根节点，记录左子树序列的长度
        int left_size = ranges::find(inorder, preorder[0]) - inorder.begin();
        // 在前序序列中找左子树
        vector<int> pre1(preorder.begin() + 1, preorder.begin() + 1 + left_size);
        // 在前序序列中找右子树
        vector<int> pre2(preorder.begin() + 1 + left_size, preorder.end());
        // 中序遍历同样的操作
        vector<int> in1(inorder.begin(), inorder.begin() + left_size);
        vector<int> in2(inorder.begin() + 1 + left_size, inorder.end());
        // 递归
        TreeNode *left = buildTree(pre1, in1);
        TreeNode *right = buildTree(pre2, in2);
        return new TreeNode(preorder[0], left, right);
    }
};

2.相同的树

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

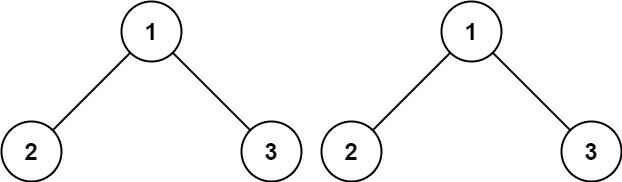
输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

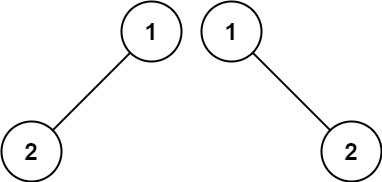
输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

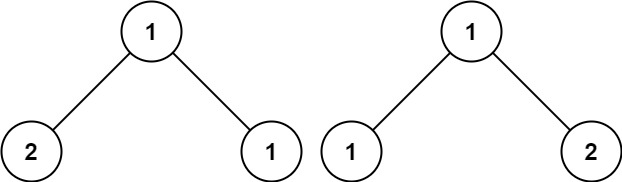
输入：p = [1,2,1], q = [1,1,2]
输出：false

提示：

两棵树上的节点数目都在范围 [0, 100] 内
-10^4 <= Node.val <= 10^4

思路

解决二叉树问题就是要灵活运用递归的性质。我们需要思考，如何将原问题分解为更小的子问题来解决，比如这道题。

要判断两棵二叉树是否相等，我们可以将它分解为以下子问题：

两棵二叉树的根节点值是否相等？
两个二叉树根节点的左边两棵子树是否相同？右边两棵子树是否相同？

分解完子问题后，我们便可以得出判断方法了：先判断根节点的值是否相等，再判断根节点的左右子树是否相等。

我们怎么判断根节点的左右子树是否相等呢？这个问题可以用递归解决。

这里需要判断出递归的边界条件：当递归到某个节点为空，就需要判断另外一个节点是否为空，如果为空，返回 true ，否则返回 false。

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if (p == nullptr || q == nullptr) return p == q;
        return p->val == q->val && isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
    }
};

3.对称二叉树

给你一个二叉树的根节点 root ，检查它是否轴对称。

示例 1：

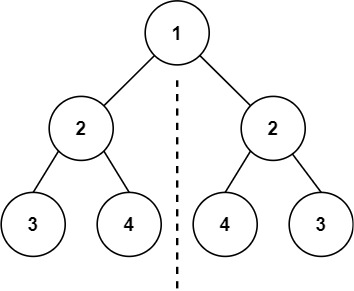
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

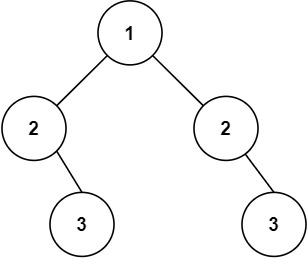
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100

思路

判断二叉树是否对称，同样需要将其分解为更小的子问题：

首先，根节点已经是对称的，可以不用管
然后需要判断根节点的左右子树是否对称

于是我们可以这样做：

把给定的树拆成左右两棵树，看根节点是否相同。
然后递归左边的左子树，和右边的右子树；以及左边的右子树和右边的左子树，看他们是否相等

这里可以直接用 T2 的代码：

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSame(TreeNode* p, TreeNode* q) {
        if (p == nullptr || q == nullptr) return p == q;
        return p->val == q->val && isSame(p->left, q->right) && isSame(p->right, q->left);
    }

    bool isSymmetric(TreeNode* root) {
        return isSame(root->left, root->right);
    }
};

4.平衡二叉树

给定一个二叉树，判断它是否是平衡二叉树

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

提示：

树中的节点数在范围 [0, 5000] 内
-10^4 <= Node.val <= 10^4

思路

要判断一棵树是否是平衡二叉树，我们需要计算这棵树的左右子树高度，再判断左右子树高度差是否大于 1 。

那么我们如何通过计算左右子树的高度来判断平衡树呢？

由于树的高度都是非负数，我们可以利用负数来表示当前子树不平衡。如果当前子树不平衡，那么包含这个子树的树也一定不平衡，直接返回即可。

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int get_height(TreeNode* p) {
        if (p == nullptr) return 0;
        // 递归计算左子树高度
        int left_height = get_height(p->left);
        // 高度为 -1 表示当前树不平衡，那么包含当前树的树也一定不平衡
        if (left_height == -1) return -1;
        // 递归计算右子树高度
        int right_height = get_height(p->right);
        if (right_height == -1 || abs(left_height - right_height) > 1) return -1;
        return max(left_height, right_height) + 1;
    }

    bool isBalanced(TreeNode* root) {
        // 如果不为 -1 ，则代表是平衡二叉树
        return get_height(root) != -1;
    }
};

5.二叉树的右视图

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1:

输入: [1,2,3,null,5,null,4]
输出: [1,3,4]

示例 2:

输入: [1,null,3]
输出: [1,3]

示例 3:

输入: []
输出: []

提示:

二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100

思路

要求二叉树的右视图数组，除了 BFS 还可以这样递归：

先不断递归二叉树的右子树，将最右侧的数字都加入到答案数组 res 中
然后递归二叉树的左子树，用一个变量 depth 记录当前递归深度，如果 depth 超出了 res 的长度，说明当前”左边的“节点没有被最右边的节点遮挡，那么将其添加到答案数组中即可

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    vector<int> res;

public:
    void dfs(TreeNode* root, int depth) {
        if (root == nullptr) return; // 递归边界
        if (depth == res.size()) res.push_back(root->val);
        dfs(root->right, depth + 1);
        dfs(root->left, depth + 1);
    }

    vector<int> rightSideView(TreeNode* root) {
        dfs(root, 0);
        return res;
    }
};

6.子结构判断

给定两棵二叉树 tree1 和 tree2，判断 tree2 是否以 tree1 的某个节点为根的子树具有 相同的结构和节点值 。注意，空树不会是以 tree1 的某个节点为根的子树具有 相同的结构和节点值 。

示例 1：

输入：tree1 = [1,7,5], tree2 = [6,1]
输出：false
解释：tree2 与 tree1 的一个子树没有相同的结构和节点值。

示例 2：

输入：tree1 = [3,6,7,1,8], tree2 = [6,1]
输出：true
解释：tree2 与 tree1 的一个子树拥有相同的结构和节点值。即 6 - > 1。

提示：

0 <= 节点个数 <= 10000

思路

如果树 B 是树 A 的子结构，则子结构的根节点可能为树 A 的任意一个节点。因此，判断树 B 是否为树 A 的子结构，需要完成以下两步工作：

先序遍历树 A 中的每个节点 node （调用函数 isSubStructure(A, B) 遍历树 A ）
判断树 A 中以 node 为根节点的子树是否包含树 B （调用函数 recur(A, B) ，判定树 A 包含树 B ）

recur(A, B) 用于进行 A 树和 B 树的匹配，判断树 A 是否包含树 B （此处的”包含“建立在树 A 和树 B 的根节点相同的条件上）

终止条件：
1. 当节点 B 为空：说明树 B 已匹配完成（越过叶子节点），因此返回 true ；
2. 当节点 A 为空：说明已经越过树 A 的叶节点，即匹配失败，返回 false ；
3. 当节点 A 和 B 的值不同：说明匹配失败，返回 false ；
返回值：
1. 判断 A 和 B 的 左子节点 是否相等，即 recur(A.left, B.left) ；
2. 判断 A 和 B 的 右子节点 是否相等，即 recur(A.right, B.right) ；

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
private:
    bool recur(TreeNode* A, TreeNode* B) {
        // A 树和 B 树从根节点开始同步往下递归
        if(B == nullptr) return true; // B 先到达空节点，说明 A 树包含 B 树
        if(A == nullptr || A->val != B->val) return false;
        return recur(A->left, B->left) && recur(A->right, B->right);
    }

public:
    bool isSubStructure(TreeNode* A, TreeNode* B) {
        return (A != nullptr && B != nullptr) && (recur(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B));
    }
};

7.翻转二叉树（二叉树的镜像）

给定一棵二叉树的根节点 root，请左右翻转这棵二叉树，并返回其根节点。

示例 1：

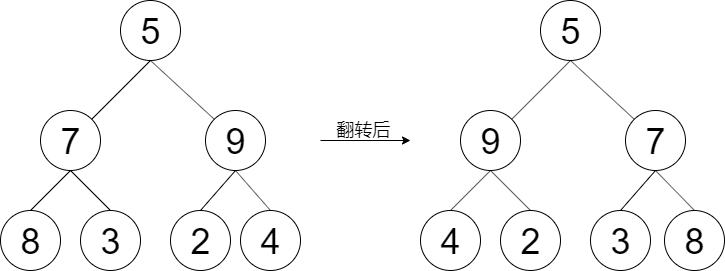
输入：root = [5,7,9,8,3,2,4]
输出：[5,9,7,4,2,3,8]

提示：

树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100

思路

对于二叉树递归问题，我们需要分析他的子问题是什么。我们要对给定的二叉树进行镜像操作，可以通过以下步骤实现：

交换根节点的左右节点
对左子树进行镜像操作
对右子树进行镜像操作

完成上面三步之后，这棵二叉树就被完全镜像了

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* mirrorTree(TreeNode* root) {
        if (!root) return root;
        TreeNode* temp = root->left;
        root->left = root->right;
        root->right = temp;
        mirrorTree(root->left);
        mirrorTree(root->right);
        return root;
    }
};

8.从上到下逐层打印二叉树Ⅰ

一棵圣诞树记作根节点为 root 的二叉树，节点值为该位置装饰彩灯的颜色编号。请按照从左到右的顺序返回每一层彩灯编号。

示例 1：

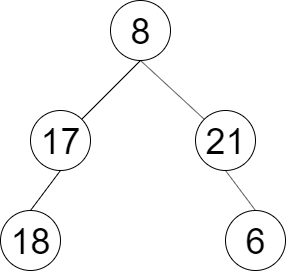
输入：root = [8,17,21,18,null,null,6]
输出：[8,17,21,18,6]

提示：

节点总数 <= 1000

思路

简单 BFS ，逐层将节点加入答案数组即可。

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> decorateRecord(TreeNode* root) {
        if (!root) return {};
        queue<TreeNode*> q;
        vector<int> res;
        q.push(root);
        while (!q.empty()) {
            TreeNode* node = q.front();
            q.pop();
            res.push_back(node->val);
            if (node->left) q.push(node->left);
            if (node->right) q.push(node->right);
        }
        return res;
    }
};

9.从上到下逐层打印二叉树Ⅱ

一棵圣诞树记作根节点为 root 的二叉树，节点值为该位置装饰彩灯的颜色编号。请按照从左到右的顺序返回每一层彩灯编号，每一层的结果记录于一行。

示例 1：

输入：root = [8,17,21,18,null,null,6]
输出：[[8],[17,21],[18,6]]

提示：

节点总数 <= 1000

思路

本题与上一题唯一不同的是需要将每层节点的值先放到一个 vector 中，再将每一层对应的 vector 压入答案数组里。因此处理队列的 while 循环里需要通过 for 循环来对每一层进行切分。

Code

class Solution {
public:
    vector<vector<int>> decorateRecord(TreeNode* root) {
        queue<TreeNode*> que;
        vector<vector<int>> res;
        if(root != NULL) que.push(root);
        while(!que.empty()) {
            vector<int> tmp;
            for(int i = que.size(); i > 0; --i) {
                root = que.front();
                que.pop();
                tmp.push_back(root->val);
                if(root->left != NULL) que.push(root->left);
                if(root->right != NULL) que.push(root->right);
            }
            res.push_back(tmp);
        }
        return res;
    }
};

10.从上到下逐层打印二叉树Ⅲ

一棵圣诞树记作根节点为 root 的二叉树，节点值为该位置装饰彩灯的颜色编号。请按照如下规则记录彩灯装饰结果：

第一层按照从左到右的顺序记录
除第一层外每一层的记录顺序均与上一层相反。即第一层为从左到右，第二层为从右到左。

示例 1：

输入：root = [8,17,21,18,null,null,6]
输出：[[8],[21,17],[18,6]]

提示：

节点总数 <= 1000

思路

在前两题的基础上，需要实现：从上往下，每层存放的节点值顺序不同，奇数层顺序存，偶数层逆序存。

本题可以通过双端队列 deque 实现。

具体实现方式看代码。

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> decorateRecord(TreeNode* root) {
        if (!root) return {};
        deque<TreeNode*> deq;
        deq.push_back(root);
        vector<vector<int>> res;
        bool ok = true; // 奇数层：true；偶数层：false
        while (!deq.empty()) {
            vector<int> temp;
            int sz = deq.size();
            if (ok) { // 若为奇数层，则顺序存储
                for (int i = 0; i < sz; ++i) {
                    TreeNode* node = deq.front();
                    temp.push_back(node->val);
                    deq.pop_front();
                    if (node->left != nullptr) deq.push_back(node->left);
                    if (node->right != nullptr) deq.push_back(node->right);
                }
                ok = false;
            } else { // 若为偶数层，则逆序存储
                for (int i = 0; i < sz; ++i) {
                    TreeNode* node = deq.back();
                    temp.push_back(node->val); // 逆序压入答案
                    deq.pop_back();
                    /*
                    对偶数层逆序存储时插入下一层需要从 deq 的前端插入
                    取到本层数据是从 deq 尾端取，从尾端插入新数据会导致本层答案错误
                    注意，为了保证从队头到队尾的顺序需要先插入右节点，再插入左节点
                    */
                    if (node->right != nullptr) deq.push_front(node->right);
                    if (node->left != nullptr) deq.push_front(node->left);
                }
                ok = true;
            }
            res.push_back(temp);
        }
        return res;
    }
};

11.验证二叉搜索树的后序遍历序列

请实现一个函数来判断整数数组 postorder 是否为二叉搜索树的后序遍历结果。

示例 1：

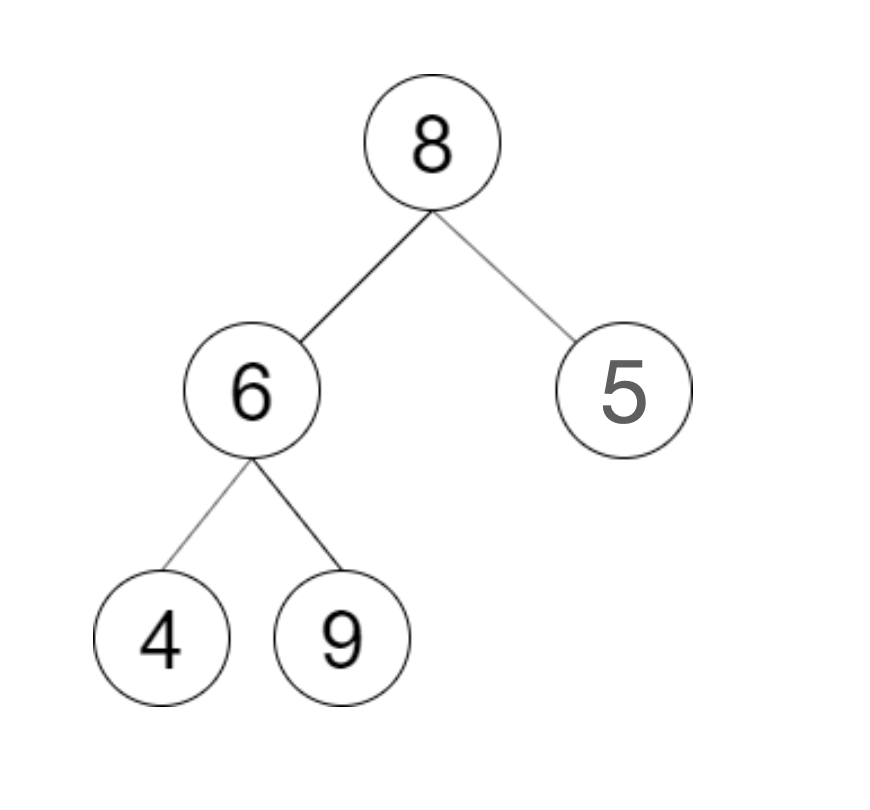
输入: postorder = [4,9,6,5,8]
输出: false 
解释：从上图可以看出这不是一颗二叉搜索树

示例 2：

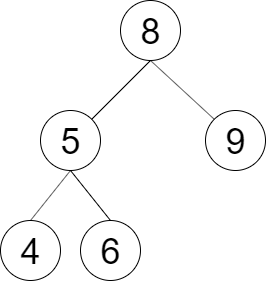
输入: postorder = [4,6,5,9,8]
输出: true 
解释：可构建的二叉搜索树如上图

提示：

数组长度 <= 1000
postorder 中无重复数字

思路

二叉树的后序遍历是：左子节点-右子节点-根节点 。

二叉搜索树的性质是：左子节点的值小于根节点，右子节点的值大于根节点，并且左右子树也都是二叉搜索树。

对于本题，我们需要：

根据后序遍历序列，
判断该树是否为二叉搜索树。

先思考第二个问题，我们如何判断一棵树是二叉搜索树？

根据二叉搜索树的性质，根节点的左右两棵子树都是二叉搜索树，并且左子节点的值小于根节点，右子节点的值大于根节点。

于是我们可以先判断左子节点、右子节点和根节点的大小关系，然后递归判断根节点的左右子树即可。

但我们现在拿到的是一个二叉树的后序遍历序列，我们怎么还原出二叉树从而进行递归呢？

由于后序遍历的顺序是 左子节点-右子节点-根节点 ，所以给定的后序序列的最后一个元素一定是整棵二叉树的根节点。

根据二叉搜索树的性质，右子节点的值一定是最大的，左子节点的值一定是最小的，并且我们知道当前二叉树的根节点，所以我们可以先把整棵树划分成：左子树部分、根节点、右子树部分。

定义：recur(postorder, i, j) 表示序列 postorder 的 [i, j] 区间是否为二叉搜索树

我们用一个指针 p 去遍历整个序列，先找到当前 [i, j] 区间第一个大于根节点的索引 m（根据后序遍历的性质，当前区间的根节点索引为 j ），此时就确定了整棵二叉树的左子树区间：[i, m-1] 。如果剩下的右子树区间：[m, j-1] 满足该区间的数都比根节点大，那么当前搜索树树的基本结构是正确的。

为什么上面说的是基本正确而不是完全正确呢？这是因为此时只能说明整棵树的根节点、根节点的左子节点、根节点的右子节点的大小顺序是正确的，但是它的左右子树不一定满足搜索树的性质。

所以我们需要递归遍历上面的左右子树区间，将这些条件联合起来判断，才能说明给定的树是否为二叉搜索树。

Code

class Solution {
public:
    bool verifyTreeOrder(vector<int>& postorder) {
        // j 表示根节点索引，i 表示后序区间最左侧
        auto recur = [&](auto&& recur, vector<int> postorder, int i, int j) -> bool {
            if (i >= j) return true;
            int p = i;
            while (postorder[p] < postorder[j]) ++p;
            int m = p; // 第一个大于根节点的索引，那么左子树区间：[i, m-1]；右子树区间：[m, j-1]
            while (postorder[p] > postorder[j]) ++p; // 循环结束后如果 p == j，那么该树是基本正确的
            return p == j && recur(recur, postorder, i, m - 1) && recur(recur, postorder, m, j - 1);
        };

        return recur(recur, postorder, 0, postorder.size() - 1);
    }
};

12.二叉树中和为目标值的路径

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：

输入：root = [1,2], targetSum = 0
输出：[]

提示：

树中节点总数在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

思路

前序遍历二叉树，回溯枚举答案即可。

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    vector<vector<int>> res;
    vector<int> path;

public:
    vector<vector<int>> pathTarget(TreeNode* root, int target) {
        auto dfs = [&](auto&& dfs, TreeNode* root, int target) {
            if (root == nullptr) return;
            path.push_back(root->val);
            target -= root->val;
            if (target == 0 && root->left == nullptr && root->right == nullptr) {
                res.push_back(path);
            }
            dfs(dfs, root->left, target);
            dfs(dfs, root->right, target);
            path.pop_back();
            target += root->val;
        };

        dfs(dfs, root, target);
        return res;
    }
};

13.将二叉搜索树转化为排序的双向链表

将一个 二叉搜索树 就地转化为一个 已排序的双向循环链表 。

对于双向循环列表，你可以将左右孩子指针作为双向循环链表的前驱和后继指针，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中最小元素的指针。

示例 1：

输入：root = [4,2,5,1,3] 

输出：[1,2,3,4,5]

解释：下图显示了转化后的二叉搜索树，实线表示后继关系，虚线表示前驱关系。

示例 2：

输入：root = [2,1,3]
输出：[1,2,3]

示例 3：

输入：root = []
输出：[]
解释：输入是空树，所以输出也是空链表。

示例 4：

输入：root = [1]
输出：[1]

提示：

-1000 <= Node.val <= 1000
Node.left.val < Node.val < Node.right.val
Node.val 的所有值都是独一无二的
0 <= Number of Nodes <= 2000

思路

题目要求将给定的二叉搜索树原地转换为已排序的双向链表，我们可以利用二叉搜索树的性质：根节点的左子树都比根节点小，右子树都比根节点大。

为了利用这个性质，我们可以中序遍历二叉树，定义前驱节点指针 pre 和当前节点指针 cur ，在遍历的过程中根据要求将节点的左右指针指向对应的节点即可。注意遍历完后还需要把双向链表的头尾节点连起来。

Code

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;

    Node() {}

    Node(int _val) {
        val = _val;
        left = NULL;
        right = NULL;
    }

    Node(int _val, Node* _left, Node* _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/
class Solution {
private:
    Node *pre, *head;

public:
    Node* treeToDoublyList(Node* root) {
        auto dfs = [&](auto&& dfs, Node* cur) {
            if (cur == nullptr) return;
            // 中序遍历
            dfs(dfs, cur->left);
            if (pre != nullptr) pre->right = cur;
            else head = cur; // 如果前序节点，说明是头节点
            cur->left = pre;
            pre = cur;
            dfs(dfs, cur->right);
        };

        if (root == nullptr) return nullptr;
        dfs(dfs, root);
        // 处理链表头尾，保证为循环链表
        head->left = pre;
        pre->right = head;
        return head;
    }
};

14.序列化与反序列化二叉树

序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。

请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

提示: 输入输出格式与 LeetCode 目前使用的方式一致，详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式，你也可以采用其他的方法解决这个问题。

示例 1：

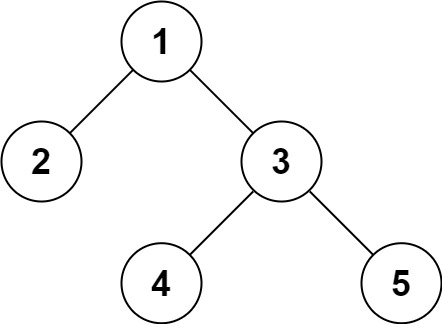
输入：root = [1,2,3,null,null,4,5]
输出：[1,2,3,null,null,4,5]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

输入：root = [1,2]
输出：[1,2]

提示：

树中结点数在范围 [0, 104] 内
-1000 <= Node.val <= 1000

思路

序列化二叉树需要对二叉树进行前序遍历，在遍历的过程中判断当前节点是否为空，如果为空就在答案字符串中添加 "None," ，否则添加节点值。

反序列化二叉树需要将字符串根据逗号分割，将分割出来的单词放到 list 中，然后递归遍历 list 构建二叉树。

注意：这里 c++ 要用 list 存放分割出来的 string 不能用 vector 。因为 list 是用双向链表实现的，适合实现增删改查，而 vector 是连续空间的数组，增删耗时较多

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Codec {
public:
    void rserialize(TreeNode* root, string& str) {
        if (root == nullptr) {
            str += "None,";
        } else {
            str += to_string(root->val) + ",";
            rserialize(root->left, str);
            rserialize(root->right, str);
        }
    }

    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {
        string res;
        rserialize(root, res);
        return res;
    }

    TreeNode* rdeserialize(list<string>& dataArray) {
        if (dataArray.front() == "None") {
            dataArray.erase(dataArray.begin());
            return nullptr;
        }

        TreeNode* root = new TreeNode(stoi(dataArray.front()));
        dataArray.erase(dataArray.begin());
        root->left = rdeserialize(dataArray);
        root->right = rdeserialize(dataArray);
        return root;
    }

    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
        list<string> dataArray;
        string str;
        for (auto& ch: data) {
            if (ch == ',') {
                dataArray.push_back(str);
                str.clear();
            } else {
                str.push_back(ch);
            }
        }
        if (!str.empty()) {
            dataArray.push_back(str);
            str.clear();
        }
        return rdeserialize(dataArray);
    }
};

// Your Codec object will be instantiated and called as such:
// Codec codec;
// codec.deserialize(codec.serialize(root));

15.寻找二叉搜索树中的目标节点

某公司组织架构以二叉搜索树形式记录，节点值为处于该职位的员工编号。请返回第 cnt 大的员工编号。

示例 1：

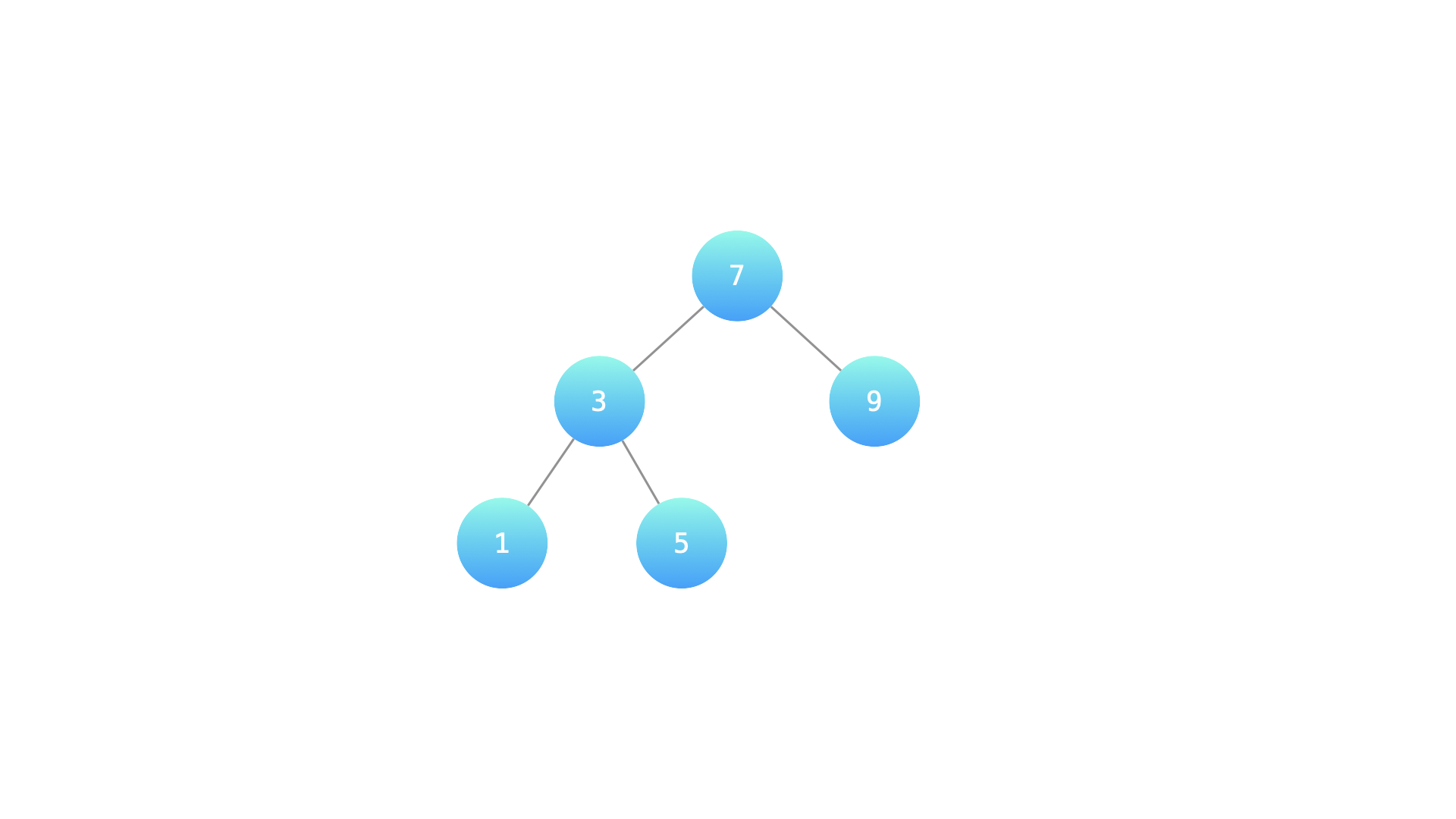
输入：root = [7, 3, 9, 1, 5], cnt = 2
       7
      / \
     3   9
    / \
   1   5
输出：7

示例 2：

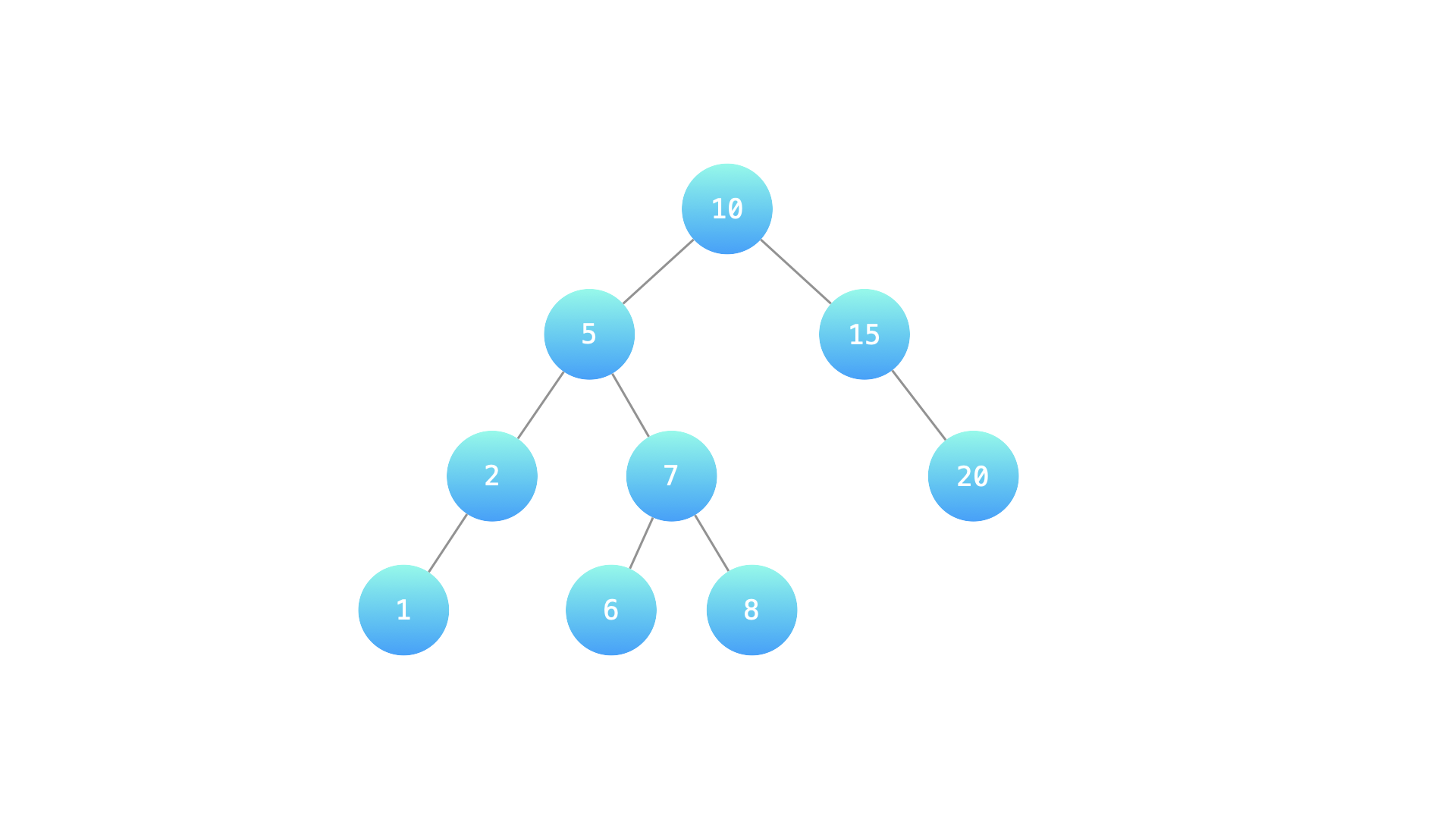
输入: root = [10, 5, 15, 2, 7, null, 20, 1, null, 6, 8], cnt = 4
       10
      / \
     5   15
    / \    \
   2   7    20
  /   / \ 
 1   6   8
输出: 8

提示：

1 ≤ cnt ≤ 二叉搜索树元素个数

思路

因为给定的是一棵二叉搜索树，我们对这棵树进行中序遍历，用一个 cnt 记录当前是第几大的节点，最终返回即可。

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    int res, cnt;

public:
    int findTargetNode(TreeNode* root, int k) {
        cnt = k;
        auto dfs = [&](auto&& dfs, TreeNode* node) {
            if (node == nullptr) return;
            dfs(dfs, node->right);
            if (cnt == 0) return;
            if (--cnt == 0) {
                res = node->val;
                return;
            }
            dfs(dfs,node->left);
        };

        dfs(dfs, root);
        return res;
    }
};

16.计算二叉树的深度

某公司架构以二叉树形式记录，请返回该公司的层级数。

示例 1：

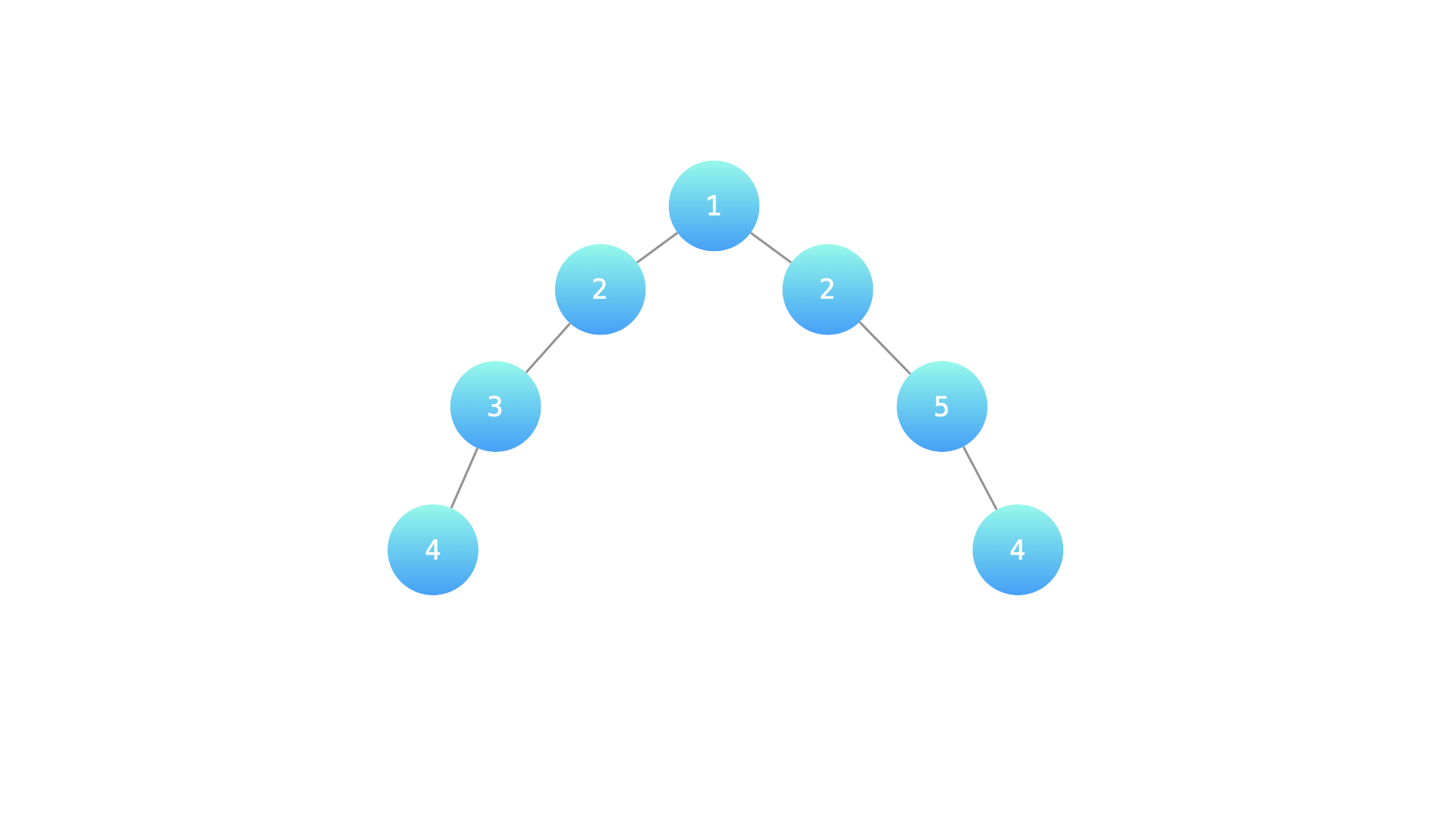
输入：root = [1, 2, 2, 3, null, null, 5, 4, null, null, 4]
输出: 4
解释: 上面示例中的二叉树的最大深度是 4，沿着路径 1 -> 2 -> 3 -> 4 或 1 -> 2 -> 5 -> 4 到达叶节点的最长路径上有 4 个节点。

思路

第一种做法是直接递归：分别递归计算左右子树高度，那么这棵树的高度就是左右子树高度的最大值 + 1 。

第二种做法是对左右子树分别 dfs ，记录下来大小然后计算高度。

Code

1.直接递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int calculateDepth(TreeNode* root) {
        if (root == nullptr) return 0;
        int l_depth = calculateDepth(root->left);
        int r_depth = calculateDepth(root->right);
        return max(l_depth, r_depth) + 1;
    }
};

2.分别 dfs 计算

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int calculateDepth(TreeNode* root) {
        auto dfs = [&](auto&& dfs, TreeNode* root, int& res, int temp) {
            if (root == nullptr) {
                res = max(res, temp);
                return;
            }
            temp++;
            dfs(dfs, root->left, res, temp);
            dfs(dfs, root->right, res, temp);
        };

        int res = 0, temp = 0;
        dfs(dfs, root, res, temp);
        return res;
    }
};

17.判断是否为平衡二叉树

输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

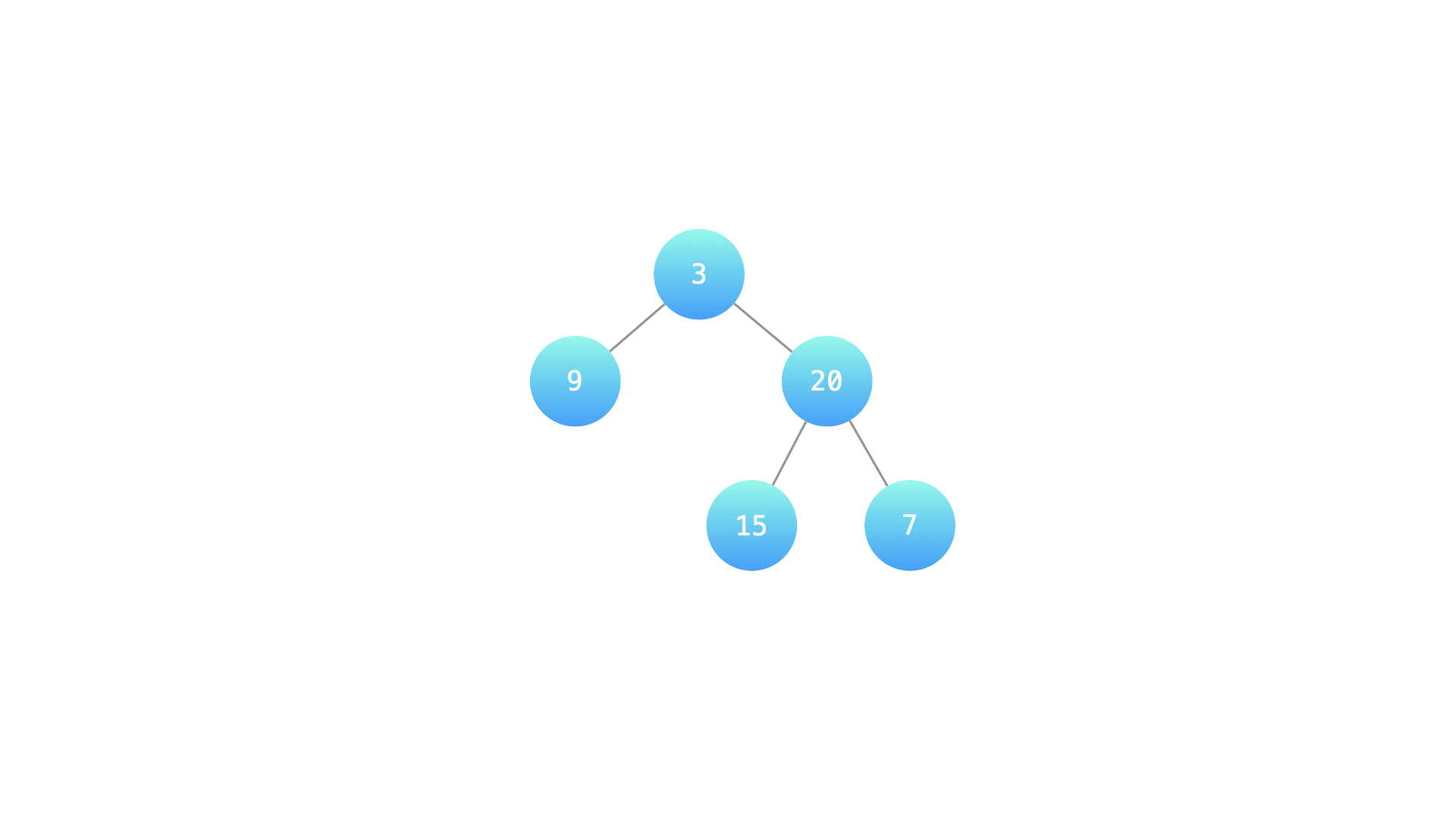
示例 1:

输入：root = [3,9,20,null,null,15,7]
输出：true 
解释：如下图

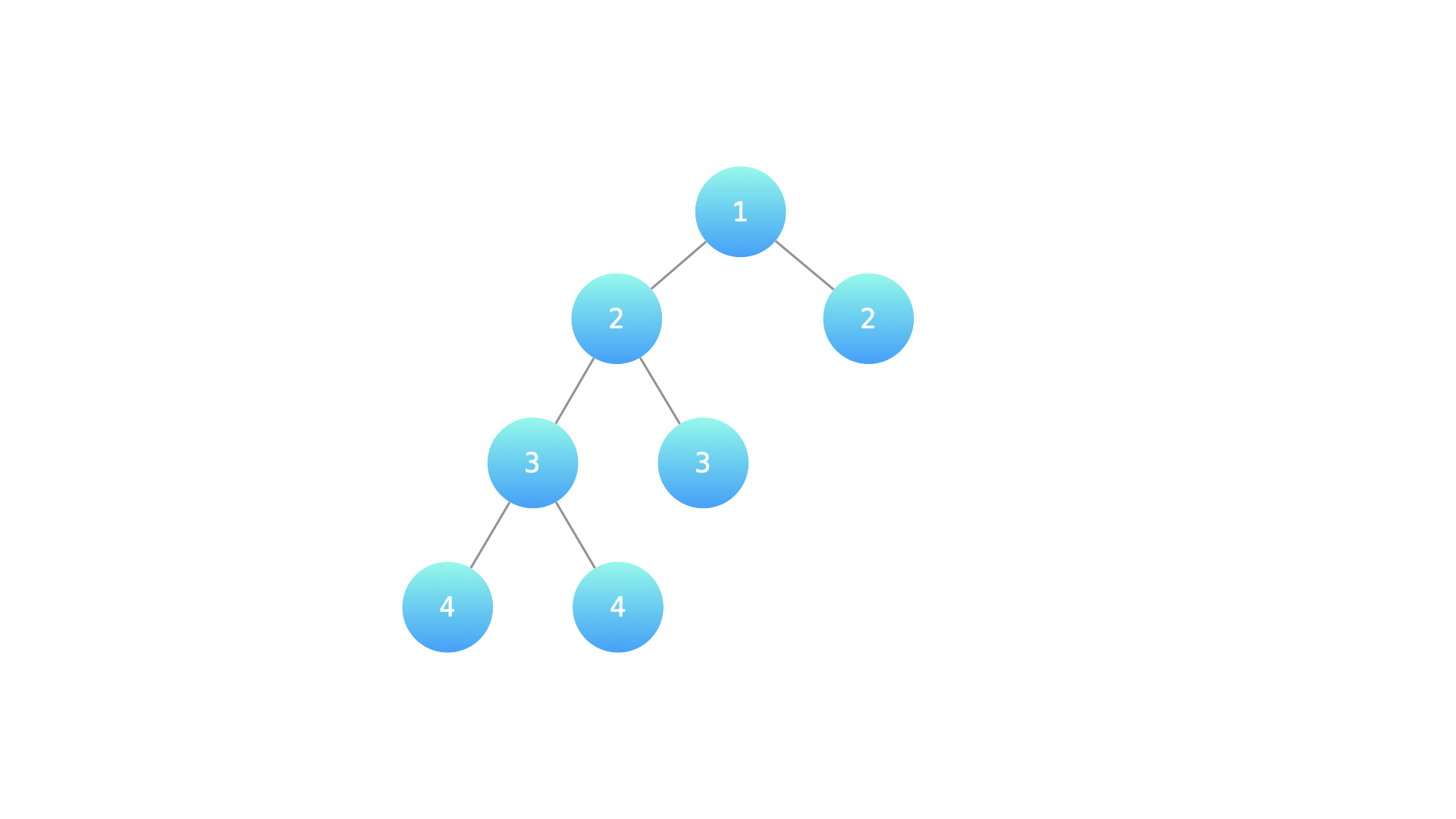
示例 2:

输入：root = [1,2,2,3,3,null,null,4,4]
输出：false
解释：如下图

提示：

0 <= 树的结点个数 <= 10000

思路

计算左右两棵子树的高度，计算两棵子树的高度差，如果大于 1 就说明这棵树不平衡。

可以在递归过程中判断当前子树是否为平衡二叉树，如果不平衡，说明整棵树不平衡，直接返回 -1 剪枝。

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        auto get_height = [&](auto&& get_height, TreeNode* node) -> int {
            if (node == nullptr) return 0;
            int leftH = get_height(get_height, node->left); // 递归计算左子树
            if (leftH == -1) return -1; // 若不平衡
            int rightH = get_height(get_height, node->right); // 递归计算右子树
            if (rightH == -1 || abs(leftH - rightH) > 1) return -1;
            return max(leftH, rightH) + 1; // 树的高度为左子树和右子树高度的最大值 + 1
        };

        return get_height(get_height, root) != -1;
    }
};

18.二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。

思路

给定的是二叉搜索树，利用它的性质分类讨论：

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        int x = root->val;
        if (p->val < x && q->val < x) // p、q都在左子树
            return lowestCommonAncestor(root->left, p, q);
        if (p->val > x && q->val > x) // p、q都在右子树
            return lowestCommonAncestor(root->right, p, q);
        return root;
    }
};

19.二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

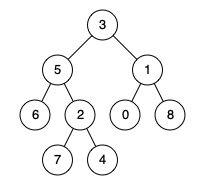
示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。

思路

相较于上一题，本题给定的是普通的二叉树，分类讨论：

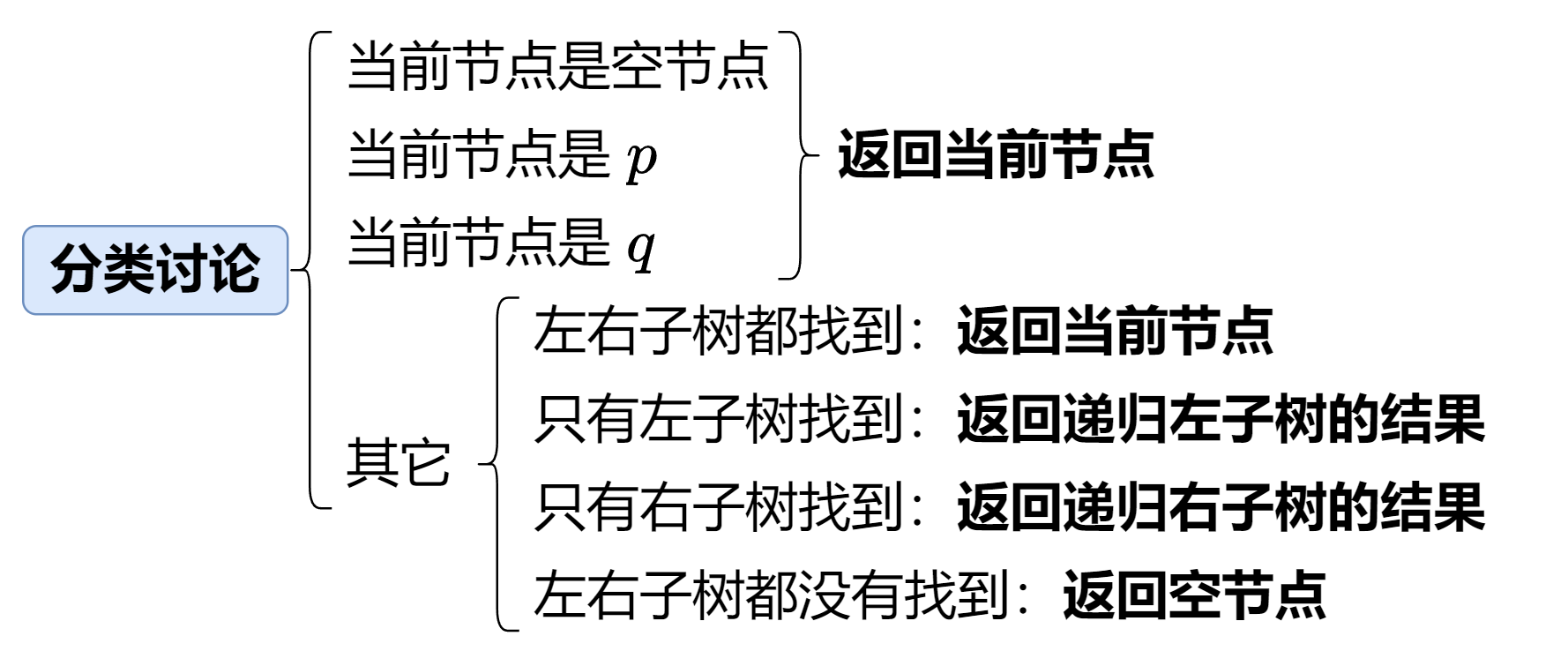
其中，左右子树都找到指的是 p 和 q 分别在当前根节点的左右子树中；只有左子树找到指的是 p 和 q 都在当前根节点的左子树中，右子树同理。对于左右子树都没有找到的情况，举个例子：当前递归的是根节点的左子树，但 p 和 q 都在根节点的右子树，所以需要返回空。

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == nullptr || root == p || root == q) return root;
        TreeNode *left = lowestCommonAncestor(root->left, p, q);
        TreeNode *right = lowestCommonAncestor(root->right, p, q);
        if (left && right) return root;
        return left ? left : right;
    }
};

YUKIPEDIA

YUKIPEDIA's blog

LCR-二叉树

目录

1.根据前序与中序遍历序列构造二叉树

2.相同的树

3.对称二叉树

4.平衡二叉树

5.二叉树的右视图

6.子结构判断

7.翻转二叉树（二叉树的镜像）

8.从上到下逐层打印二叉树Ⅰ

9.从上到下逐层打印二叉树Ⅱ

10.从上到下逐层打印二叉树Ⅲ

11.验证二叉搜索树的后序遍历序列

12.二叉树中和为目标值的路径

13.将二叉搜索树转化为排序的双向链表

14.序列化与反序列化二叉树

15.寻找二叉搜索树中的目标节点

16.计算二叉树的深度

17.判断是否为平衡二叉树

18.二叉搜索树的最近公共祖先

19.二叉树的最近公共祖先