1.找出最具竞争力的子序列(单调栈+贪心)
给你一个整数数组 nums 和一个正整数 k ,返回长度为 k 且最具 竞争力 的 nums 子序列。
数组的子序列是从数组中删除一些元素(可能不删除元素)得到的序列。
在子序列 a 和子序列 b 第一个不相同的位置上,如果 a 中的数字小于 b 中对应的数字,那么我们称子序列 a 比子序列 b(相同长度下)更具 竞争力 。 例如,[1,3,4] 比 [1,3,5] 更具竞争力,在第一个不相同的位置,也就是最后一个位置上, 4 小于 5 。
示例 1:
输入:nums = [3,5,2,6], k = 2
输出:[2,6]
解释:在所有可能的子序列集合 {[3,5], [3,2], [3,6], [5,2], [5,6], [2,6]} 中,[2,6] 最具竞争力。
示例 2:
输入:nums = [2,4,3,3,5,4,9,6], k = 4
输出:[2,3,3,4]
提示:
1 <= nums.length <= 10^50 <= nums[i] <= 10^91 <= k <= nums.length
思路
根据题意,最具竞争力的子序列一定是较小的元素尽可能地放到序列的前面。所以我们可以遍历一遍数组,维持一个单调栈结构,将较小的元素尽可能地往前放。
那么我们应该如何操作?因为我们可以使用单调栈,所以说我们每次将当前元素和栈顶元素比较,如果当前元素更小,并且能够保证栈内元素数目 + 数组中剩余元素 > k且栈非空,那么我们就弹出栈顶元素,将当前元素压入栈,一直重复,最后返回栈内自下而上的前k各元素为结果即可。
记nums的大小为n,遍历数组nums,假设当前访问的下标为 i ,对数组nums[i]执行以下操作:
- 记栈中元素数目为 m,我们不断地进行操作直到不满足以下条件:如果 m > 0且 m + n - i > k且单调栈的栈顶元素大于nums[i],说明栈顶元素可以被当前数字nums[i]替换,我们就弹出栈顶元素
- 将nums[i]压入栈中
- 最后返回栈自下而上的前 k 个元素作为结果
代码如下
class Solution {
public:
vector<int> mostCompetitive(vector<int>& nums, int k) {
vector<int> res;
int n = nums.size(); // 原数组的大小
for (int i = 0; i < n; ++i) {
while (!res.empty() && res.size() + n - i > k && res.back() > nums[i]) {
res.pop_back();
}
res.push_back(nums[i]);
}
res.resize(k);
return res;
}
};
2.搜索插入位置(二分搜索)
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
提示:
1 <= nums.length <= 10^4-10^4 <= nums[i] <= 10^4nums为 无重复元素 的 升序 排列数组-10^4 <= target <= 10^4
思路
不断用二分法逼近查找第一个大于等于target的下标,ans初值设置为数组长度可以省略边界条件的判断,因为存在一种情况是target大于数组中的所有数,此时需要插入到数组长度的位置
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int left = 0, right = nums.size() - 1;
int ans = nums.size();
while (left <= right) {
// 防止加法溢出,位运算比除法更快
int middle = ((right - left) >> 1 ) + left;
if (target > nums[middle]) {
left = middle + 1;
} else if (target <= nums[middle]) {
ans = middle; // 将目标数字插到middle的位置
right = middle - 1;
}
}
return ans;
}
};
3.删除并获得点数(打家劫舍)
给你一个整数数组 nums ,你可以对它进行一些操作。
每次操作中,选择任意一个 nums[i] ,删除它并获得 nums[i] 的点数。之后,你必须删除 所有 等于 nums[i] - 1 和 nums[i] + 1 的元素。
开始你拥有 0 个点数。返回你能通过这些操作获得的最大点数。
示例 1:
输入:nums = [3,4,2]
输出:6
解释:
删除 4 获得 4 个点数,因此 3 也被删除。
之后,删除 2 获得 2 个点数。总共获得 6 个点数。
示例 2:
输入:nums = [2,2,3,3,3,4]
输出:9
解释:
删除 3 获得 3 个点数,接着要删除两个 2 和 4 。
之后,再次删除 3 获得 3 个点数,再次删除 3 获得 3 个点数。
总共获得 9 个点数。
提示:
1 <= nums.length <= 2 * 10^41 <= nums[i] <= 10^4
思路
题目中的条件:“每次操作中,选择任意一个 nums[i] ,删除它并获得 nums[i] 的点数。之后,你必须删除 所有 等于 nums[i] - 1 和 nums[i] + 1 的元素”,可以理解为打家劫舍。
记元素x在数组中出现的次数为cx,我们可以用一个数组sum记录数组nums中所有相同元素之和,即sum[x] = x * cx。若选择了x,则可以获取sum[x]的点数,且无法再选择x-1和x+1。
class Solution {
public:
int rob(vector<int> &sum) {
int size = sum.size();
int dp[size];
dp[0] = sum[0];
dp[1] = max(sum[0], sum[1]);
for (int i = 2; i < size; ++i) {
dp[i] = max(dp[i - 1], dp[i - 2] + sum[i]);
}
return dp[size - 1];
}
int deleteAndEarn(vector<int>& nums) {
int maxVal = 0;
for (auto val : nums) maxVal = max(maxVal, val);
vector<int> sum(maxVal + 1);
for (auto val : nums) sum[val] += val;
return rob(sum);
}
};
由于在打家劫舍中,每个变量的状态只与前两个变量的状态有关,所以可以不使用数组,只用两个变量来实现。
class Solution {
public:
int rob(vector<int> &nums) {
int size = nums.size();
int first = nums[0], second = max(nums[0], nums[1]);
for (int i = 2; i < size; i++) {
int temp = second;
second = max(first + nums[i], second);
first = temp;
}
return second;
}
int deleteAndEarn(vector<int>& nums) {
int maxVal = 0;
for (auto val : nums) maxVal = max(maxVal, val);
vector<int> sum(maxVal + 1);
for (auto val : nums) sum[val] += val;
return rob(sum);
}
};
4.K 秒后第 N 个元素的值(前缀和)
给你两个整数 n 和 k。
最初,你有一个长度为 n 的整数数组 a,对所有 0 <= i <= n - 1,都有 a[i] = 1 。每过一秒,你会同时更新每个元素为其前面所有元素的和加上该元素本身。例如,一秒后,a[0] 保持不变,a[1] 变为 a[0] + a[1],a[2] 变为 a[0] + a[1] + a[2],以此类推。
返回 k 秒后 a[n - 1] 的值。
由于答案可能非常大,返回其对 109 + 7 取余 后的结果。
示例 1:
输入:n = 4, k = 5
输出:56
解释:
| 时间(秒) | 数组状态 |
|---|---|
| 0 | [1,1,1,1] |
| 1 | [1,2,3,4] |
| 2 | [1,3,6,10] |
| 3 | [1,4,10,20] |
| 4 | [1,5,15,35] |
| 5 | [1,6,21,56] |
示例 2:
输入:n = 5, k = 3
输出:35
解释:
| 时间(秒) | 数组状态 |
|---|---|
| 0 | [1,1,1,1,1] |
| 1 | [1,2,3,4,5] |
| 2 | [1,3,6,10,15] |
| 3 | [1,4,10,20,35] |
提示:
1 <= n, k <= 1000
思路
注意每次计算前缀和后取余,不要最后返回结果的时候取余,不然会爆longlong。还有一点就是不能暴力遍历,会超时,所以需要用dp
class Solution {
public:
int valueAfterKSeconds(int n, int k) {
int mod = 1e9 + 7;
long long a[n];
for (int i = 0; i < n; ++i) a[i] = 1;
while (k--) {
long long sum[1005] = {1};
for (int i = 1; i < n; ++i) {
sum[i] = sum[i - 1] + a[i];
sum[i] %= mod;
}
for (int i = 0; i < n; ++i) {
a[i] = sum[i];
}
}
return a[n - 1];
}
};
5.救生艇(双指针+贪心)
给定数组 people 。people[i]表示第 i 个人的体重 ,船的数量不限,每艘船可以承载的最大重量为 limit。
每艘船最多可同时载两人,但条件是这些人的重量之和最多为 limit。
返回 承载所有人所需的最小船数 。
示例 1:
输入:people = [1,2], limit = 3
输出:1
解释:1 艘船载 (1, 2)
示例 2:
输入:people = [3,2,2,1], limit = 3
输出:3
解释:3 艘船分别载 (1, 2), (2) 和 (3)
示例 3:
输入:people = [3,5,3,4], limit = 5
输出:4
解释:4 艘船分别载 (3), (3), (4), (5)
提示:
1 <= people.length <= 5 * 10^41 <= people[i] <= limit <= 3 * 10^4
思路
本题是较明显的贪心问题。要承载所有人所需的船数尽可能的小,就需要每艘船装的人尽量多。怎么装才能使人尽量多呢?自然而然是把体重大的和体重小的安排在同一艘船上。所以贪心选择策略是:每艘船装当前最大体重和最小体重的人,如果总体重超过limit,则大体重的自己上一艘船,小体重和下一个大体重的匹配。实现这个策略可以使用双指针,在此之前我们需要people数组有序。
class Solution {
public:
int numRescueBoats(vector<int>& people, int limit) {
int ans = 0;
int num = people.size();
sort(people.begin(), people.end(), greater<int>());
int left = 0, right = num - 1;
while (left <= right) {
ans++;
if (left == right) break;
if (people[left] + people[right] <= limit) {
left++, right--;
} else {
left++;
}
}
return ans;
}
};
6.甲板上的战舰
给你一个大小为 m x n 的矩阵 board 表示甲板,其中,每个单元格可以是一艘战舰 'X' 或者是一个空位 '.' ,返回在甲板 board 上放置的 战舰 的数量。
战舰 只能水平或者垂直放置在 board 上。换句话说,战舰只能按 1 x k(1 行,k 列)或 k x 1(k 行,1 列)的形状建造,其中 k 可以是任意大小。两艘战舰之间至少有一个水平或垂直的空位分隔 (即没有相邻的战舰)。
示例 1:
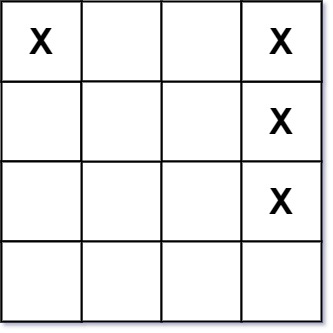
输入:board = [["X",".",".","X"],[".",".",".","X"],[".",".",".","X"]]
输出:2
示例 2:
输入:board = [["."]]
输出:0
提示:
m == board.lengthn == board[i].length1 <= m, n <= 200board[i][j]是'.'或'X'
思路
遍历一次board,找到一个X就遍历行和列,将X改为.,统计答案即可
class Solution {
public:
int countBattleships(vector<vector<char>>& board) {
int row = board.size();
int col = board[0].size();
int ans = 0;
for (int i = 0; i < row; ++i) {
for (int j = 0; j < col; ++j) {
if (board[i][j] == 'X') {
board[i][j] = '.';
// 遍历列
for (int k = j + 1; k < col && board[i][k] == 'X'; ++k)
board[i][k] = '.';
// 遍历行
for (int k = i + 1; k < row && board[k][j] == 'X'; ++k)
board[k][j] = '.';
ans++;
}
}
}
return ans;
}
};
7.不同路径Ⅱ
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
示例 2:

输入:obstacleGrid = [[0,1],[0,0]]
输出:1
提示:
m == obstacleGrid.lengthn == obstacleGrid[i].length1 <= m, n <= 100obstacleGrid[i][j]为0或1
思路
这是一个带障碍物的二维dp,我们可以将其降到一维,代码如下
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int n = obstacleGrid.size(), m = obstacleGrid.at(0).size();
vector<int> dp(m); // 用一维数组遍历整个棋盘
if (obstacleGrid[0][0] == 0) dp[0] = 1;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (obstacleGrid[i][j] == 1) {
dp[j] = 0;
continue;
}
if (j - 1 >= 0 && obstacleGrid[i][j - 1] == 0) {
dp[j] += dp[j - 1]; // 这里的dp[j]是继承了上一行的dp[j],所以只用加上前一个dp[j - 1]即可
}
}
}
return dp.back();
}
};
二维做法如下
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size(), n = obstacleGrid.at(0).size();
int dp[105][105] = {0};
if (obstacleGrid[0][0] == 0) dp[0][0] = 1; // 特判一下起点
for (int i = 1; i < n; ++i) {
if (obstacleGrid[0][i] != 1) dp[0][i] += dp[0][i - 1];
else dp[0][i] = 0;
}
for (int j = 1; j < m; ++j) {
if (obstacleGrid[j][0] != 1) dp[j][0] += dp[j - 1][0];
else dp[j][0] = 0;
}
for (int i = 1; i < m; ++i) {
for (int j = 1; j < n; ++j) {
if (obstacleGrid[i][j] == 1) dp[i][j] = 0;
else dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};
8.施咒的最大总伤害(dp)
一个魔法师有许多不同的咒语。
给你一个数组 power ,其中每个元素表示一个咒语的伤害值,可能会有多个咒语有相同的伤害值。
已知魔法师使用伤害值为 power[i] 的咒语时,他们就 不能 使用伤害为 power[i] - 2 ,power[i] - 1 ,power[i] + 1 或者 power[i] + 2 的咒语。
每个咒语最多只能被使用 一次 。
请你返回这个魔法师可以达到的伤害值之和的 最大值 。
示例 1:
输入:power = [1,1,3,4]
输出:6
解释:
可以使用咒语 0,1,3,伤害值分别为 1,1,4,总伤害值为 6 。
示例 2:
输入:power = [7,1,6,6]
输出:13
解释:
可以使用咒语 1,2,3,伤害值分别为 1,6,6,总伤害值为 13 。
提示:
1 <= power.length <= 10^51 <= power[i] <= 10^9
思路
本题为动态规划,每个咒语都有一个对应的伤害值,选了某个咒语后,该咒语的伤害值+-2范围内的咒语都不能选,给定一个咒语数组,要我们求最大能够造成多少伤害。注意若有多个相同伤害值的咒语,可以重复选择。所以对于每种伤害值的咒语,他能打出的伤害应该是ai*bi,其中ai表示咒语的伤害值,bi表示该伤害值咒语的数量。
我们用f[i]来记录最后使用第i个咒语能打出的最大总伤害,我们先根据咒语的本身基础伤害排序,那么对于j<i,有下面的状态转移方程:f[i] = f[j] + ai*bi,其中要满足aj < ai - 2。
class Solution {
public:
long long maximumTotalDamage(vector<int>& power) {
map<int, int>mp; // 统计每种伤害值咒语的个数
for (auto x : power) mp[x]++;
typedef pair<int, int> pii;
// vec里按伤害从小到大保存每种咒语的伤害和数量
vector<pii> vec;
vec.push_back(pii(-1e9, 0));
for (auto &p : mp) vec.push_back(p);
int n = vec.size();
// f[i]表示最后释放了第i种咒语的最大总伤害
long long f[n];
f[0] = 0;
long long mx = 0;
// 计算释放第i个咒语能获得的最大伤害
for (int i = 1, j = 1; i < n; ++i) {
// 求当前满足条件的最大伤害
while (j < i && vec[j].first < vec[i].first - 2) {
mx = max(mx, f[j]);
++j;
}
// 释放第i个咒语的伤害+之前能达到的最大伤害 = 释放第i个咒语所能达到的最大伤害
f[i] = mx + 1LL * vec[i].first * vec[i].second;
}
long long ans = 0;
// 求最大值返回
for (int i = 1; i < n; ++i) ans = max(ans, f[i]);
return ans;
}
};
9.构成整天的下标对数目(哈希表)
给你一个整数数组 hours,表示以 小时 为单位的时间,返回一个整数,表示满足 i < j 且 hours[i] + hours[j] 构成 整天 的下标对 i, j 的数目。
整天 定义为时间持续时间是 24 小时的 整数倍 。
例如,1 天是 24 小时,2 天是 48 小时,3 天是 72 小时,以此类推。
示例 1:
输入: hours = [12,12,30,24,24]
输出: 2
解释:
构成整天的下标对分别是 (0, 1) 和 (3, 4)。
示例 2:
输入: hours = [72,48,24,3]
输出: 3
解释:
构成整天的下标对分别是 (0, 1)、(0, 2) 和 (1, 2)。
提示:
1 <= hours.length <= 5 * 10^51 <= hours[i] <= 10^9
思路
看数据范围直接进行枚举会超时,这里采用哈希表查找,本题的思路和两数之和差不多。
我们遍历一遍数组,计算当前遍历到的元素对24的余数p,那么他所需要配对的数字的余数就应该是(24 - p) % 24,记录配对的次数即可
class Solution {
public:
long long countCompleteDayPairs(vector<int>& hours) {
unordered_map <int, int> map_cnt;
long long ans = 0;
for (auto hour : hours) {
int p = hour % 24; // 当前的余数
int q = (24 - p) % 24; // 需要的余数
if (map_cnt.find(q) != map_cnt.end()) {
ans += map_cnt[q];
}
map_cnt[p]++;
}
return ans;
}
};
10.最大正方形
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
示例 1:

输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:4
示例 2:

输入:matrix = [["0","1"],["1","0"]]
输出:1
示例 3:
输入:matrix = [["0"]]
输出:0
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 300matrix[i][j]为'0'或'1'
思路
我们定义dp[i][j]表示以(i, j)为右下角,且只包含1的正方形边长的最大值。
-
如果该位置的值为0,则
dp[i][j] = 0,因为当前位置不可能在由1组成的正方形中 -
如果该位置为1,则
dp[i][j]的值由其上方、左方和左下方的三个相邻的dp值决定,具体而言,当前位置的元素值等于三个相邻位置的元素中的最小值加1,状态转移方程如下dp[i][j] = min({dp[i-1][j], dp[i][j-1], dp[i-1][j-1]}) + 1
下面给出证明
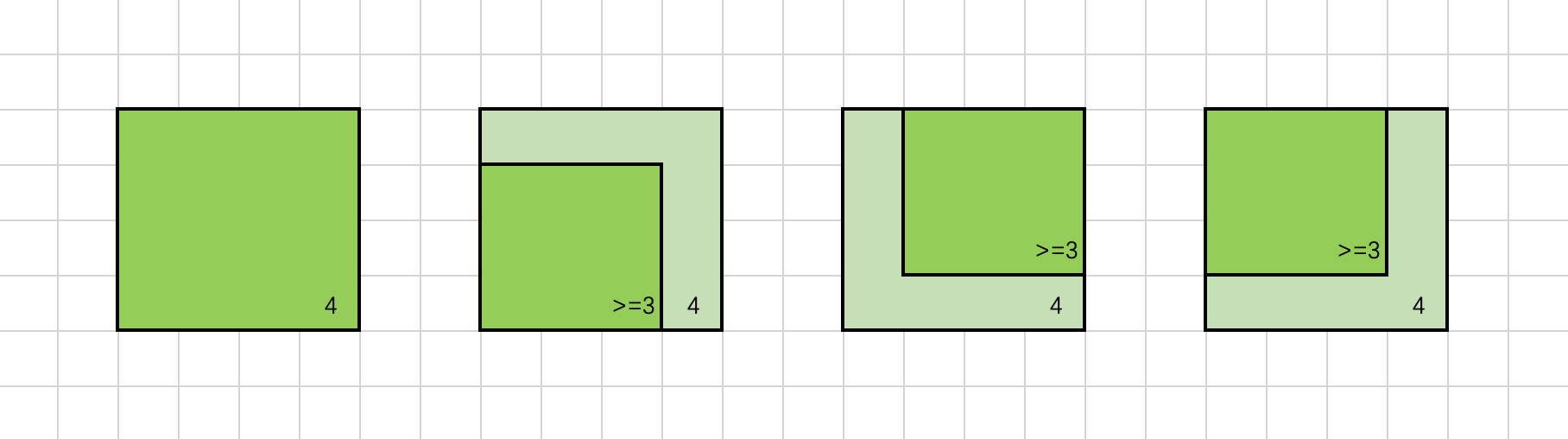
如上图所示,若对于(i, j)有dp[i][j] = 4,我们将以(i, j)为右下角、边长为4的正方形涂上颜色,可以发现其左侧位置(i, j-1),上方位置(i-1, j),左上方位置(i-1, j-1)均可以作为一个边长为4 - 1 = 3的正方形的右下角。也就是说,这些位置的dp值至少为3,即:
dp[i][j-1] >= dp[i][j] - 1dp[i-1][j] >= dp[i][j] - 1dp[i-1][j-1] >= dp[i][j] - 1
联立以上三个不等式,得到:
min({dp[i][j-1], dp[i-1][j], dp[i-1][j-1]}) >= dp[i][j] - 1
以上推导过程是我们通过固定dp[i][j]的值,判断其相邻位置与之的关系得到的不等式。同理,我们也能固定dp[i][j]相邻位置的值,得到另外的限制条件。
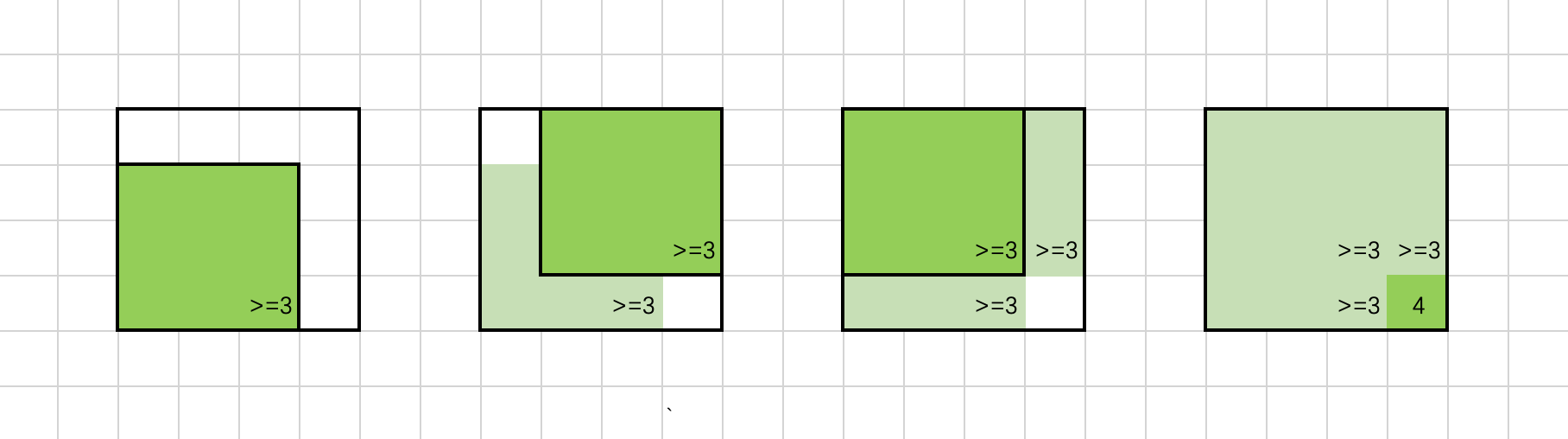
如上图所示,假设dp[i][j-1],dp[i-1][j]和dp[i-1][j-1]中最小值为3,
也就是说(i, j-1)、(i-1, j)和(i-1, j-1)均可以作为一个边长为3的正方形的右下角。
我们将这些边长为3的正方形依次涂上色,可以发现如果(i, j)的元素为1,那么它可以作为一个边长为4的正方形的右下角,dp值至少为4,即:
dp[i][j] >= min() + 1
联立两种情况得到的不等式,可以得到状态转移方程
dp[i][j] = min() + 1
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
if (matrix.size() == 0 || matrix[0].size() == 0) return 0;
int ans = 0;
int row = matrix.size(), col = matrix[0].size();
vector<vector<int>> dp(row, vector<int>(col));
for (int i = 0; i < row; ++i) {
for (int j = 0; j < col; ++j) {
if (matrix[i][j] == '1') {
if (i == 0 || j == 0) dp[i][j] = 1;
else dp[i][j] = min({dp[i-1][j], dp[i][j-1], dp[i-1][j-1]}) + 1;
}
ans = ans > dp[i][j] ? ans : dp[i][j];
}
}
return ans * ans;
}
};
11.最长回文子序列
给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
示例 1:
输入:s = "bbbab"
输出:4
解释:一个可能的最长回文子序列为 "bbbb" 。
示例 2:
输入:s = "cbbd"
输出:2
解释:一个可能的最长回文子序列为 "bb" 。
提示:
1 <= s.length <= 1000s仅由小写英文字母组成
思路
动态规划,我们定义dp[i][j]表示s串第i到第j位的最大回文子序列长度,对于每个较短的子序列s[i+1...j-1],都可以通过向其首部和尾部添加遍历到的字符来进行状态转移。
- 如果当前首部和尾部字符相同,则可以添加
dp[i][j] = dp[i+1][j-1] + 2
- 如果首部和尾部字符不同,则不能添加
dp[i][j] = max(dp[i+1][j], dp[i][j-1])
class Solution {
public:
int longestPalindromeSubseq(string s) {
int len = s.length();
// dp[i][j]表示s串下标从i到j的最长回文子序列长度
vector<vector<int>> dp(len, vector<int>(len));
for (int i = len - 1; i >= 0; --i) {
dp[i][i] = 1; // 长度为1是回文子序列
char c1 = s[i];
for (int j = i + 1; j < len; ++j) {
char c2 = s[j];
// 首尾相同,可以添加
if (c1 == c2) dp[i][j] = dp[i+1][j-1] + 2;
// 首尾不同,不能添加
else dp[i][j] = max(dp[i+1][j], dp[i][j-1]);
}
}
return dp[0][len-1];
}
};
12.找出有效子序列的最大长度(dp)
给你一个整数数组 nums 和一个 正 整数 k 。
nums 的一个 子序列sub 的长度为 x ,如果其满足以下条件,则称其为 有效子序列 :
(sub[0] + sub[1]) % k == (sub[1] + sub[2]) % k == ... == (sub[x - 2] + sub[x - 1]) % k
返回 nums 的 最长有效子序列 的长度。
注:子序列 是可以通过从另一个数组删除或不删除某些元素,但不更改其余元素的顺序得到的数组。
示例 1:
输入:nums = [1,2,3,4,5], k = 2
输出:5
解释:
最长有效子序列是 [1, 2, 3, 4, 5] 。
示例 2:
输入:nums = [1,4,2,3,1,4], k = 3
输出:4
解释:
最长有效子序列是 [1, 4, 1, 4] 。
提示:
2 <= nums.length <= 10^31 <= nums[i] <= 10^71 <= k <= 10^3
思路
我们先将K特殊化,假设K = 10,子序列中sub[0] = 2, sub[1] = 3,那么(sub[0] + sub[1]) % 10 = 5。根据模运算的分配律,我们可以推出sub[2] % 10 = 2,同时也有sub[3] % 10 = 3…

所以我们可以得出这个结论:子序列的奇数项模K是一样的,子序列的偶数项模K是一样的。
根据上面的结论,我们又可以推出,这两个结论:
- 当我们知道了子序列的前两个数,就知道了整个子序列
- 当我们知道了子序列的后两个数,就知道了整个子序列
于是我们就将原问题转换成了:求序列最后两个数模K为y和x的子序列长度。
我们要求解这个原问题,就是求解它的子问题:求序列最后两个数模K为x和y的子序列长度。在这个子问题的基础上+1即可得到以y和x结尾的子序列的长度。于是就有了下面的状态转移方程:
dp[y][x] = dp[x][y] + 1
然后用两层循环遍历0...k-1即可
class Solution {
public:
int maximumLength(vector<int>& nums, int k) {
// dp[y][x]表示序列最后两个数模 k 为 y 和 x 的子序列的长度
vector<vector<int>> dp(k, vector<int>(k));
for (auto y:nums) {
y %= k;
for (int x = 0; x < k; ++x)
dp[y][x] = dp[x][y] + 1;
}
int ans = INT_MIN;
for (int i = 0; i < k; ++i)
for (int j = 0; j < k; ++j)
ans = max(ans, dp[i][j]);
return ans;
}
};
13.最后一块石头的重量Ⅱ
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎; - 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
示例 1:
输入:stones = [2,7,4,1,8,1]
输出:1
解释:
组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
示例 2:
输入:stones = [31,26,33,21,40]
输出:5
提示:
1 <= stones.length <= 301 <= stones[i] <= 100
思路
本题的意思是要将原来的石头尽可能分成重量接近的两堆,然后进行粉碎就可以得到最终最小的重量。
可以通过01背包来解决:定义dp[i]为背包容量为i的背包能装的最大重量,我们先计算石头的总重量sum,然后目标是target=sum/2,需要求出容量为target的背包所能装的最大重量,求出后将两部分相减即可。
class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
vector<int> dp(15001, 0);
int sum = 0;
for (auto i:stones) sum += i;
int target = sum / 2;
for (int i = 0; i < stones.size(); ++i)
for (int j = target; j >= stones[i]; --j)
dp[j] = max(dp[j], dp[j-stones[i]] + stones[i]);
return sum - dp[target] - dp[target];
}
};
至于为什么是sum - dp[target] - dp[target],这是因为target = sum / 2是向下取整的,一定有sum - dp[target] >= dp[target]。
14.目标和
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1
输出:1
提示:
1 <= nums.length <= 200 <= nums[i] <= 10000 <= sum(nums[i]) <= 1000-1000 <= target <= 1000
思路
根据题意,我们需要在每个元素前添加 + 或 - 。所以我们可以把原集合分为两种集合:加法集合 add **与减法集合 sub **,在加法集合中,所有的元素前添加 + ,在减法集合中,所有的元素前添加 - 。
假设原集合的所有元素和为 sum ,我们有:add + sub = sum ,并且有 add - sub = target 。所以 sub = add - target ,将上式代入第一个式子,得到 2*add - target = sum ,于是乎 add = (target + sum) / 2。其中,target 和 sum 都是定值,我们只需要在原集合中找出一个子集,满足该子集和 add 等于 (target + sum) / 2 。
这就转换成了一个01背包问题:给定一个 nums 集合,给定一个背包容量 bagSize = (target + sum) / 2 ,求有多少种组合能够装满容量为bagSize 的背包。
定义 dp[i] 表示装满容量为 i 的背包有多少种方法。那么对于遍历到的数字 nums[j] ,有 dp[i] += dp[i-nums[j]] ,解释为:装满容量为 i 的背包的方法数量可以由装满容量为 i - nums[j] 的背包的方法数量推过来。
所以我们需要遍历所有物品,将 dp[i-nums[j]] 累加起来,最终得到 dp[bagSize] 。
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum = 0;
for (auto i : nums) sum += i;
if (abs(target) > sum) return 0; // target 绝对值比 sum 还大,无解
if ((target+sum) % 2 == 1) return 0; // 如果无法除尽,表示无解
int bagSize = (target + sum) / 2;
vector<int> dp(bagSize + 1, 0);
dp[0] = 1; // 注意 dp[0] 要初始化为 1 ,否则 dp 数组一直为 0
for (int i = 0; i < nums.size(); ++i) {
for (int j = bagSize; j >= nums[i]; --j) {
dp[j] += dp[j-nums[i]];
}
}
return dp[bagSize];
}
};
15.重新放置石块
给你一个下标从 0 开始的整数数组 nums ,表示一些石块的初始位置。再给你两个长度 相等 下标从 0 开始的整数数组 moveFrom 和 moveTo 。
在 moveFrom.length 次操作内,你可以改变石块的位置。在第 i 次操作中,你将位置在 moveFrom[i] 的所有石块移到位置 moveTo[i] 。
完成这些操作后,请你按升序返回所有 有 石块的位置。
注意:
- 如果一个位置至少有一个石块,我们称这个位置 有 石块。
- 一个位置可能会有多个石块。
示例 1:
输入:nums = [1,6,7,8], moveFrom = [1,7,2], moveTo = [2,9,5]
输出:[5,6,8,9]
解释:一开始,石块在位置 1,6,7,8 。
第 i = 0 步操作中,我们将位置 1 处的石块移到位置 2 处,位置 2,6,7,8 有石块。
第 i = 1 步操作中,我们将位置 7 处的石块移到位置 9 处,位置 2,6,8,9 有石块。
第 i = 2 步操作中,我们将位置 2 处的石块移到位置 5 处,位置 5,6,8,9 有石块。
最后,至少有一个石块的位置为 [5,6,8,9] 。
示例 2:
输入:nums = [1,1,3,3], moveFrom = [1,3], moveTo = [2,2]
输出:[2]
解释:一开始,石块在位置 [1,1,3,3] 。
第 i = 0 步操作中,我们将位置 1 处的石块移到位置 2 处,有石块的位置为 [2,2,3,3] 。
第 i = 1 步操作中,我们将位置 3 处的石块移到位置 2 处,有石块的位置为 [2,2,2,2] 。
由于 2 是唯一有石块的位置,我们返回 [2] 。
提示:
1 <= nums.length <= 10^51 <= moveFrom.length <= 10^5moveFrom.length == moveTo.length1 <= nums[i], moveFrom[i], moveTo[i] <= 10^9- 测试数据保证在进行第
i步操作时,moveFrom[i]处至少有一个石块。
思路
本题简单来讲,是给你一个原始数组和两个移动数组,根据两个移动数组将原始数组中的数字进行依次替换,最后返回升序排列。
考虑到返回升序排列,我们可以用 set 容器实现升序。
需要注意的是,当我们想通过迭代器修改集合中的元素,不能像数组中的下标访问一样根据索引访问数据,而是先删除原始数据再插入新数据。
class Solution {
public:
vector<int> relocateMarbles(vector<int>& nums, vector<int>& moveFrom, vector<int>& moveTo) {
set<int> num_set;
for (auto i: nums) num_set.insert(i);
int len = moveFrom.size();
for (int i = 0; i < len; ++i) {
auto index = num_set.find(moveFrom[i]);
num_set.erase(index); // 通过迭代器先删除原始数据
num_set.insert(moveTo[i]); // 再插入新数据
}
vector<int> ans;
for (auto i: num_set) ans.push_back(i);
return ans;
}
};
16.解决智力问题
跳过问题 i ,你可以对下一个问题决定使用哪种操作。
-
比方说,给你
questions = [[3, 2], [4, 3], [4, 4], [2, 5]]- 如果问题
0被解决了, 那么你可以获得3分,但你不能解决问题1和2。 - 如果你跳过问题
0,且解决问题1,你将获得4分但是不能解决问题2和3。
- 如果问题
请你返回这场考试里你能获得的 最高 分数。
示例 1:
输入:questions = [[3,2],[4,3],[4,4],[2,5]]
输出:5
解释:解决问题 0 和 3 得到最高分。
- 解决问题 0 :获得 3 分,但接下来 2 个问题都不能解决。
- 不能解决问题 1 和 2
- 解决问题 3 :获得 2 分
总得分为:3 + 2 = 5 。没有别的办法获得 5 分或者多于 5 分。
示例 2:
输入:questions = [[1,1],[2,2],[3,3],[4,4],[5,5]]
输出:7
解释:解决问题 1 和 4 得到最高分。
- 跳过问题 0
- 解决问题 1 :获得 2 分,但接下来 2 个问题都不能解决。
- 不能解决问题 2 和 3
- 解决问题 4 :获得 5 分
总得分为:2 + 5 = 7 。没有别的办法获得 7 分或者多于 7 分。
提示:
1 <= questions.length <= 10^5questions[i].length == 21 <= pointsi, brainpoweri <= 10^5
思路
首先尝试用 dp[i] 表示解决前 i 道题可以获得的最高分数。根据是否选择解决第 i 题,会有以下两种情况:
- 不解决第
i题,此时dp[i] = dp[i-1]; - 解决第
i题,此时要么前面的题目都未解决,要么上一道解决的题目对应的冷冻期已经结束。
由于每道题对应的冷冻期都不一样,因此我们很难在不通过遍历 [0, i-1] 闭区间内的全部下标,以判断对应的冷冻期是否结束的情况下更新 dp[i] 。如果题目总数为 n 那么时间复杂度就为 O(n^2) ,不符合题目要求。
因此我们从无后效性的角度考虑 dp 数组的定义。对于每一道题目,解决与否会影响到后面一定数量题目的结果,但不会影响到前面题目的解决。因此我们可以考虑从反方向定义状态,即考虑解决每道题本身及以后的题目可以获得的最高分数。
无后效性:某阶段的状态一旦确定,则此后过程的决策不再受此前各种状态及决策的影响
于是我们定义 dp[i] 表示解决第 i 道题及以后的题目可以获得的最高分数。同时我们从后往前遍历题目,并更新 dp 数组。类似的,根据是否选择解决第 i 道题,会有以下两种情况:
- 不解决第
i题,此时dp[i] = dp[i+1]; - 解决第
i题,我们只能解决下标大于i+brainpower[i]的题目,而此时需要根据dp数组的定义,解决这些题目的最高分数为dp[i+brainpower[i]+1]。
因此,我们有:dp[i] = points[i] + dp[i+brainpower[i]+1] 。综合上述两种情况,我们能够得出状态转移方程:dp[i] = max(dp[i+1], points[i]+dp[i+brainpower[i]+1])
另外还需要考虑 i >= n 的边界条件,代码如下
class Solution {
public:
long long mostPoints(vector<vector<int>>& questions) {
int n = questions.size();
vector<long long> dp(n+1);
for (int i = n-1; i >= 0; --i)
dp[i] = max(dp[i+1], questions[i][0]+dp[min(n, i+questions[i][1]+1)]);
return dp[0];
}
};
17.生成特殊数字的最少操作
给你一个下标从 0 开始的字符串 num ,表示一个非负整数。
在一次操作中,您可以选择 num 的任意一位数字并将其删除。请注意,如果你删除 num 中的所有数字,则 num 变为 0。
返回最少需要多少次操作可以使 num 变成特殊数字。
如果整数 x 能被 25 整除,则该整数 x 被认为是特殊数字。
示例 1:
输入:num = "2245047"
输出:2
解释:删除数字 num[5] 和 num[6] ,得到数字 "22450" ,可以被 25 整除。
可以证明要使数字变成特殊数字,最少需要删除 2 位数字。
示例 2:
输入:num = "2908305"
输出:3
解释:删除 num[3]、num[4] 和 num[6] ,得到数字 "2900" ,可以被 25 整除。
可以证明要使数字变成特殊数字,最少需要删除 3 位数字。
示例 3:
输入:num = "10"
输出:1
解释:删除 num[0] ,得到数字 "0" ,可以被 25 整除。
可以证明要使数字变成特殊数字,最少需要删除 1 位数字。
提示
1 <= num.length <= 100num仅由数字'0'到'9'组成num不含任何前导零
思路
一个数能被 25 整除,只需满足下列条件:
- 如果是 1 位数,那么就是 0
- 如果是 2 位数或者更多位数,那么它的最后两位必须是 00、25、50、75 中的一个
我们观察第二种情况,可以得出我们只需要判断数字的最后两位即可。所以我们考虑从右往左遍历,当找到 0 或 5 的时候标记一下,继续往前找对应的数字,具体情况如下图:
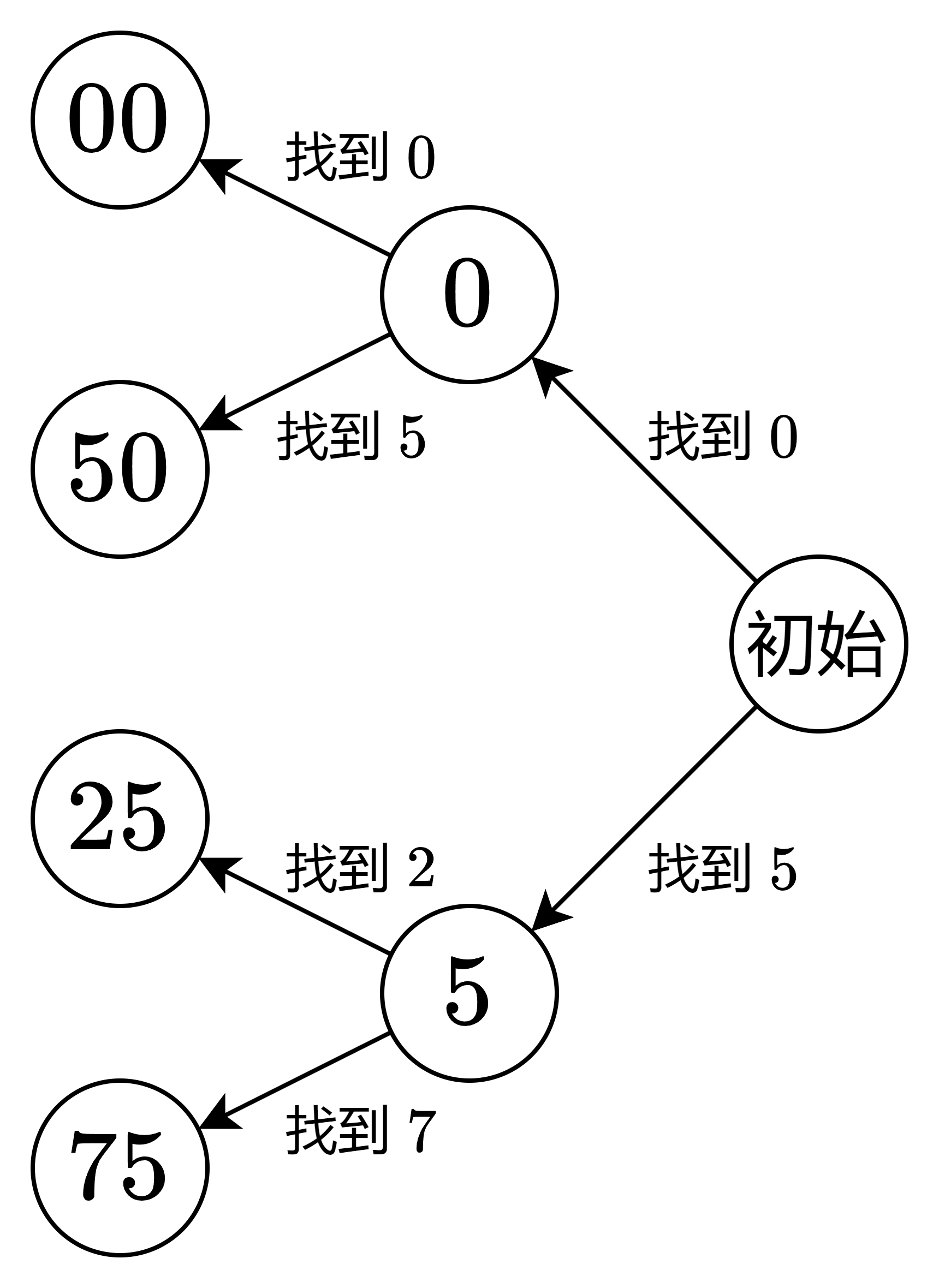
当我们找到满足条件的内容时,直接返回 n - i - 2 , i 是当前遍历到的数字下标。至于为什么是 n - i - 2 ,因为 n - i 表示从第 i 位到数字末尾的长度,再 -2 表示在这段长度中减去满足条件的两个数字,即:00、25、50、75
class Solution {
public:
int minimumOperations(string num) {
int n = num.length();
bool found0 = false, found5 = false;
for (int i = n - 1; i >= 0; i--) {
char c = num[i];
if (found0 && (c == '0' || c == '5') ||
found5 && (c == '2' || c == '7')) {
return n - i - 2;
}
if (c == '0') {
found0 = true;
} else if (c == '5') {
found5 = true;
}
}
return n - found0;
}
};
18.掉落的方块
在二维平面上的 x 轴上,放置着一些方块。
给你一个二维整数数组 positions ,其中 positions[i] = [lefti, sideLengthi] 表示:第 i 个方块边长为 sideLengthi ,其左侧边与 x 轴上坐标点 lefti 对齐。
每个方块都从一个比目前所有的落地方块更高的高度掉落而下。方块沿 y 轴负方向下落,直到着陆到 另一个正方形的顶边 或者是 x 轴上 。一个方块仅仅是擦过另一个方块的左侧边或右侧边不算着陆。一旦着陆,它就会固定在原地,无法移动。
在每个方块掉落后,你必须记录目前所有已经落稳的 方块堆叠的最高高度 。
返回一个整数数组 ans ,其中 ans[i] 表示在第 i 块方块掉落后堆叠的最高高度。
示例 1:
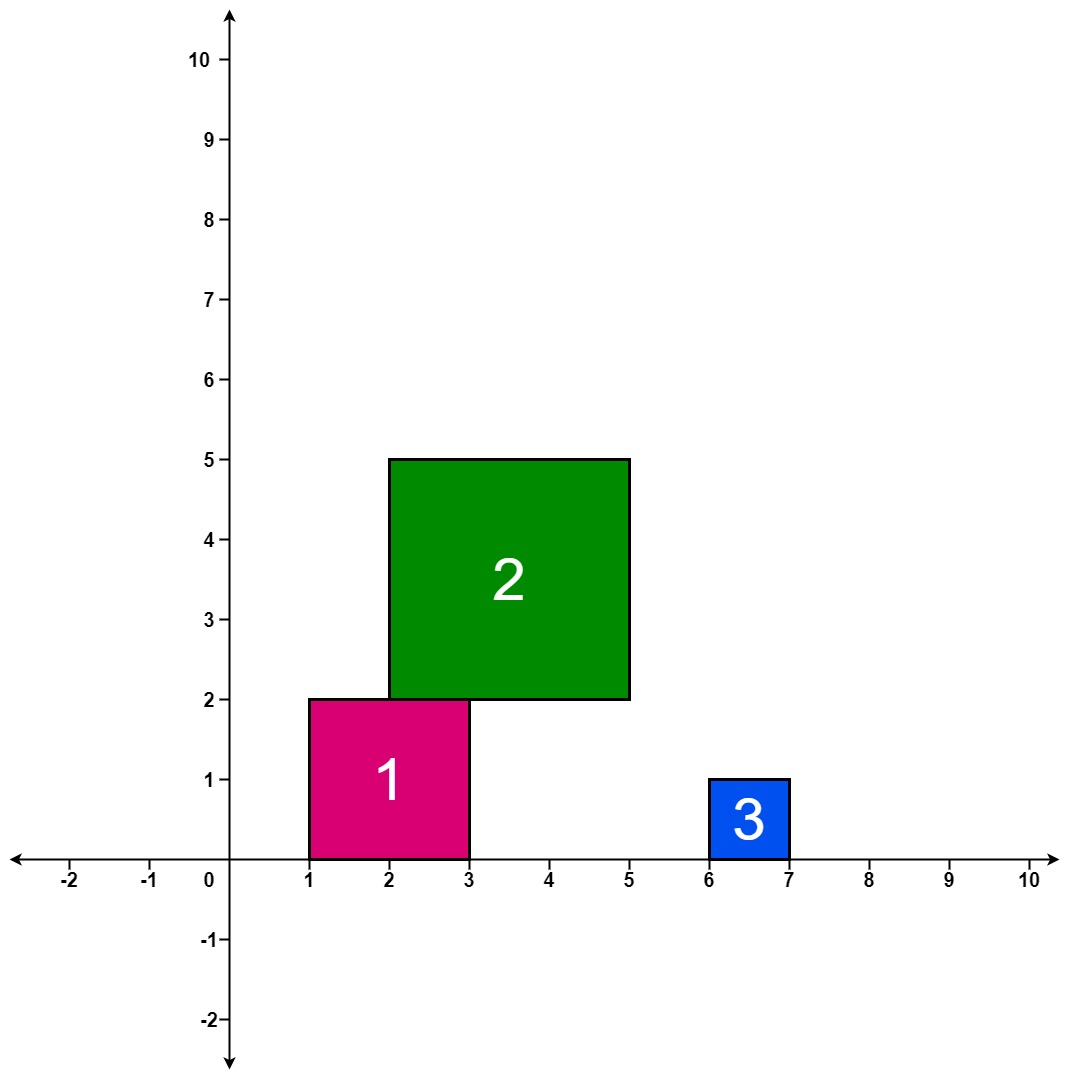
输入:positions = [[1,2],[2,3],[6,1]]
输出:[2,5,5]
解释:
第 1 个方块掉落后,最高的堆叠由方块 1 组成,堆叠的最高高度为 2 。
第 2 个方块掉落后,最高的堆叠由方块 1 和 2 组成,堆叠的最高高度为 5 。
第 3 个方块掉落后,最高的堆叠仍然由方块 1 和 2 组成,堆叠的最高高度为 5 。
因此,返回 [2, 5, 5] 作为答案。
示例 2:
输入:positions = [[100,100],[200,100]]
输出:[100,100]
解释:
第 1 个方块掉落后,最高的堆叠由方块 1 组成,堆叠的最高高度为 100 。
第 2 个方块掉落后,最高的堆叠可以由方块 1 组成也可以由方块 2 组成,堆叠的最高高度为 100 。
因此,返回 [100, 100] 作为答案。
注意,方块 2 擦过方块 1 的右侧边,但不会算作在方块 1 上着陆。
提示:
1 <= positions.length <= 10001 <= lefti <= 10^81 <= sideLengthi <= 10^6
思路
数据量不是很大,我们顺序遍历每个方块,对于每个方块再从头开始枚举已经稳定下来的方块,判断两个方块是否有重合,如果有就更新当前方块的最大高度即可。
class Solution {
public:
vector<int> fallingSquares(vector<vector<int>>& positions) {
int n = positions.size();
vector<int> height(n);
for (int i = 0; i < n; ++i) {
// 当前方块的左右边界
int left1 = positions[i][0], right1 = positions[i][0] + positions[i][1] - 1;
height[i] = positions[i][1];
// 从头开始枚举,判断当前方块与前面稳定的方块是否有重叠
for (int j = 0; j < i; ++j) {
int left2 = positions[j][0], right2 = positions[j][0] + positions[j][1] - 1;
// 如果有重叠,更新最大答案
if (right1 >= left2 && right2 >= left1) {
height[i] = max(height[i], height[j] + positions[i][1]);
}
}
}
// 最后更新一遍当前最大高度
for (int i = 1; i < n; ++i) {
height[i] = max(height[i], height[i-1]);
}
return height;
}
};
19.另一棵树的子树
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
示例 1:
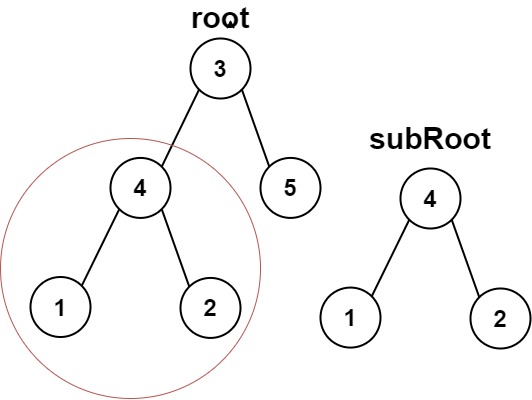
输入:root = [3,4,5,1,2], subRoot = [4,1,2]
输出:true
示例 2:
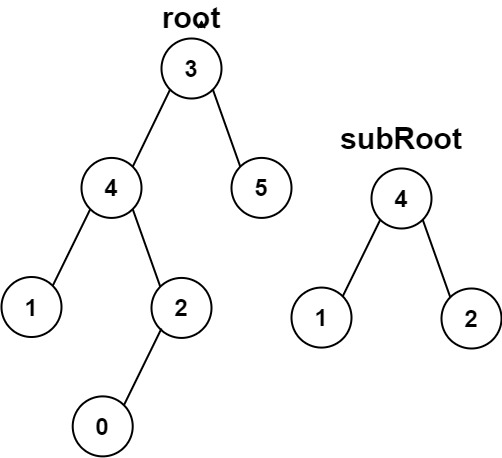
输入:root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出:false
提示:
root树上的节点数量范围是[1, 2000]subRoot树上的节点数量范围是[1, 1000]-10^4 <= root.val <= 10^4-10^4 <= subRoot.val <= 10^4
思路
数据范围不是很大,直接 dfs 判断是否有子树和另一棵树相等即可
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
// 检查两棵树是否相等
bool check(TreeNode* o, TreeNode* t) {
if (!o && !t) return true;
if ((o && !t) || (!o && t) || (o->val != t->val)) return false;
return check(o->left, t->left) && check(o->right, t->right);
}
bool dfs(TreeNode* o, TreeNode* t) {
if (!o) return false;
// 两棵树相等或者 o 的某棵子树和 t 相等
return check(o, t) || dfs(o->left, t) || dfs(o->right, t);
}
bool isSubtree(TreeNode* root, TreeNode* subRoot) {
return dfs(root, subRoot);
}
};
20.新增道路查询后的最短距离Ⅰ
给你一个整数 n 和一个二维整数数组 queries。
有 n 个城市,编号从 0 到 n - 1。初始时,每个城市 i 都有一条单向道路通往城市 i + 1( 0 <= i < n - 1)。
queries[i] = [ui, vi] 表示新建一条从城市 ui 到城市 vi 的单向道路。每次查询后,你需要找到从城市 0 到城市 n - 1 的最短路径的长度。
返回一个数组 answer,对于范围 [0, queries.length - 1] 中的每个 i,answer[i] 是处理完前 i + 1 个查询后,从城市 0 到城市 n - 1 的最短路径的长度。
示例 1:
输入: n = 5, queries = [[2, 4], [0, 2], [0, 4]]
输出: [3, 2, 1]
解释:

新增一条从 2 到 4 的道路后,从 0 到 4 的最短路径长度为 3。

新增一条从 0 到 2 的道路后,从 0 到 4 的最短路径长度为 2。

新增一条从 0 到 4 的道路后,从 0 到 4 的最短路径长度为 1。
示例 2:
输入: n = 4, queries = [[0, 3], [0, 2]]
输出: [1, 1]
解释:

新增一条从 0 到 3 的道路后,从 0 到 3 的最短路径长度为 1。

新增一条从 0 到 2 的道路后,从 0 到 3 的最短路径长度仍为 1。
提示:
3 <= n <= 5001 <= queries.length <= 500queries[i].length == 20 <= queries[i][0] < queries[i][1] < n1 < queries[i][1] - queries[i][0]- 查询中没有重复的道路。
思路
本题数据量不大,主要是熟悉 bfs 的使用
class Solution {
public:
int bfs(int n, const vector<vector<int>>& city) {
// dist[i] 表示从第 0 个城市到达第 i 个城市所需要的最短距离
vector<int> dist(n, -1);
queue<int> q;
q.push(0);
dist[0] = 0;
while (!q.empty()) {
// 当前城市能够到达的城市
int u = q.front();
q.pop();
for (int v: city[u]) {
// 未访问过就更新
// 这里这样判断是因为我们是从前往后遍历城市的,当这个城市在前面被访问过,
// 那么从当前这个点再到这个城市的距离就会更大
if (dist[v] == -1) {
dist[v] = dist[u] + 1;
q.push(v);
}
}
}
return dist[n - 1];
}
vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) {
// 城市 i 能到达的城市
vector<vector<int>> city(n);
vector<int> ans;
for (int i = 0; i < n - 1; ++i) city[i].push_back(i + 1);
// 处理每次询问
for (auto &q : queries) {
// 对应城市加上能到达的城市
city[q[0]].push_back(q[1]);
// bfs 一次
ans.push_back(bfs(n, city));
}
return ans;
}
};
21.判断子序列
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
进阶:
如果有大量输入的 S,称作 S1, S2, … , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
致谢:
特别感谢 @pbrother 添加此问题并且创建所有测试用例。
示例 1:
输入:s = "abc", t = "ahbgdc"
输出:true
示例 2:
输入:s = "axc", t = "ahbgdc"
输出:false
提示:
0 <= s.length <= 1000 <= t.length <= 10^4- 两个字符串都只由小写字符组成。
思路
首先,如果 s 是空串,直接返回 true ,因为空串是任何字符串的子序列。
如果 s 不是空串,我们可以遍历 t ,在遍历的过程中看能否匹配 s 中的每个字母。按照子序列的定义,在遍历 t 的过程中,把没匹配到的字母删除,剩下得就是匹配的字母,即字符串 s ,这就说明 s 是 t 的子序列。
具体算法如下:
- 初始化
i = 0。 - 遍历字符串
t中的字符c = t[j],看其是否与s[i]匹配,如果匹配就把i加一。加一后,如果i等于s的长度,说明s的所有字符匹配完毕,s是t的子序列,返回true。 - 如果遍历中没有返回,说明
s不是t的子序列,返回false。
代码如下:
class Solution {
public:
bool isSubsequence(string s, string t) {
if (s.empty()) return true;
int i = 0;
for (auto c: t) if (s[i] == c && ++i == s.length()) return true;
return false;
}
};
22.找出与数组相加的整数Ⅱ
给你两个整数数组 nums1 和 nums2。
从 nums1 中移除两个元素,并且所有其他元素都与变量 x 所表示的整数相加。如果 x 为负数,则表现为元素值的减少。
执行上述操作后,nums1 和 nums2 相等 。当两个数组中包含相同的整数,并且这些整数出现的频次相同时,两个数组 相等 。
返回能够实现数组相等的 最小 整数 x 。
示例 1:
输入:nums1 = [4,20,16,12,8], nums2 = [14,18,10]
输出:-2
解释:
移除 nums1 中下标为 [0,4] 的两个元素,并且每个元素与 -2 相加后,nums1 变为 [18,14,10] ,与 nums2 相等。
示例 2:
输入:nums1 = [3,5,5,3], nums2 = [7,7]
输出:2
解释:
移除 nums1 中下标为 [0,3] 的两个元素,并且每个元素与 2 相加后,nums1 变为 [7,7] ,与 nums2 相等。
提示:
3 <= nums1.length <= 200nums2.length == nums1.length - 20 <= nums1[i], nums2[i] <= 1000- 测试用例以这样的方式生成:存在一个整数
x,nums1中的每个元素都与x相加后,再移除两个元素,nums1可以与nums2相等。
思路
把两个数组都从小到大排序。
由于只能移除两个元素,所以 nums1 的前三小元素必定有一个是保留下来的,我们可以枚举保留下来的最小元素是 nums1[0] 还是 nums1[1] 还是 nums1[2] 。
注意:保留下来的最小元素绝不可能是 nums1[3] 或更大的数,因为这意味着我们把前三小的数都移除了,而题目要求只能移除两个元素。
例如排序后 nums1 = [2, 5, 6, 7, 8, 10] ,nums2 = [3, 4, 5, 8] ,如果 nums1 中保留下来的最小元素是 nums1[1] = 5 ,那么 x = nums2[0] - nums[1] = 3 - 5 = -2 ,这意味着我们把 nums1 的每个数都加上 x = -2 ,得到 nums1' = [0, 3, 4, 5, 6, 8] ,问题就变成判断 nums2 是否为 nums1' 的子序列,如果是子序列,那么就可以移除多余的两个数了。判断是否是子序列参照上一题 T21.
class Solution {
public:
int minimumAddedInteger(vector<int>& nums1, vector<int>& nums2) {
sort(nums1.begin(), nums1.end());
sort(nums2.begin(), nums2.end());
// 前三小的数一定有一个保留下来,枚举留下来的数
for (int i = 2; i > 0; --i) {
int x = nums2[0] - nums1[i];
int j = 0;
// 判断子序列
for (int k = i; k < nums1.size(); ++k) {
if (nums2[j] == nums1[k] + x && ++j == nums2.size()) return x;
}
}
return nums2[0] - nums1[0];
}
};
23.统计好节点的数目(建树+dfs)
现有一棵 无向 树,树中包含 n 个节点,按从 0 到 n - 1 标记。树的根节点是节点 0 。给你一个长度为 n - 1 的二维整数数组 edges,其中 edges[i] = [ai, bi] 表示树中节点 ai 与节点 bi 之间存在一条边。
如果一个节点的所有子节点为根的子树包含的节点数相同,则认为该节点是一个 好节点。
返回给定树中 好节点 的数量。
子树 指的是一个节点以及它所有后代节点构成的一棵树。
示例 1:
输入:edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
输出:7
说明:
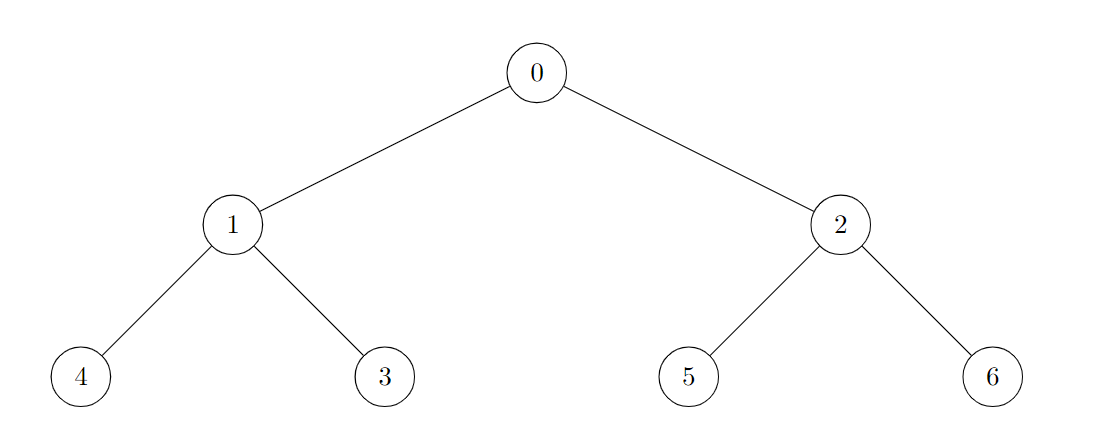
树的所有节点都是好节点。
示例 2:
输入:edges = [[0,1],[1,2],[2,3],[3,4],[0,5],[1,6],[2,7],[3,8]]
输出:6
说明:
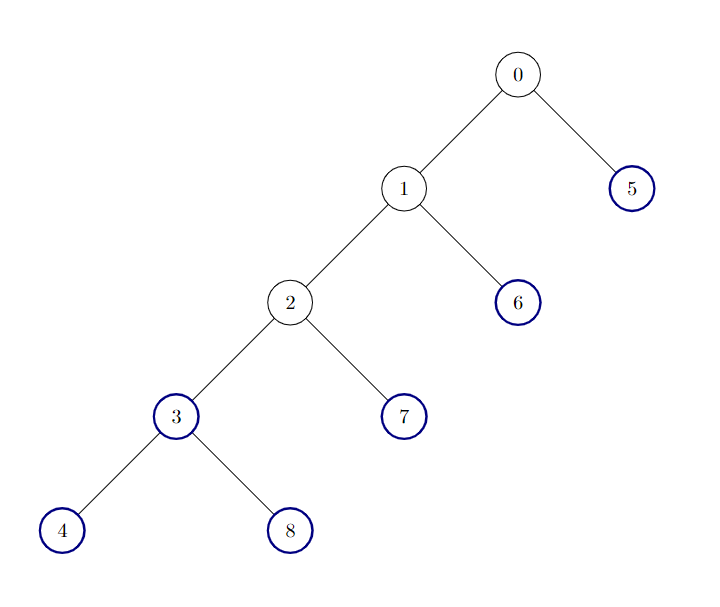
树中有 6 个好节点。上图中已将这些节点着色。
示例 3:
输入:edges = [[0,1],[1,2],[1,3],[1,4],[0,5],[5,6],[6,7],[7,8],[0,9],[9,10],[9,12],[10,11]]
输出:12
解释:
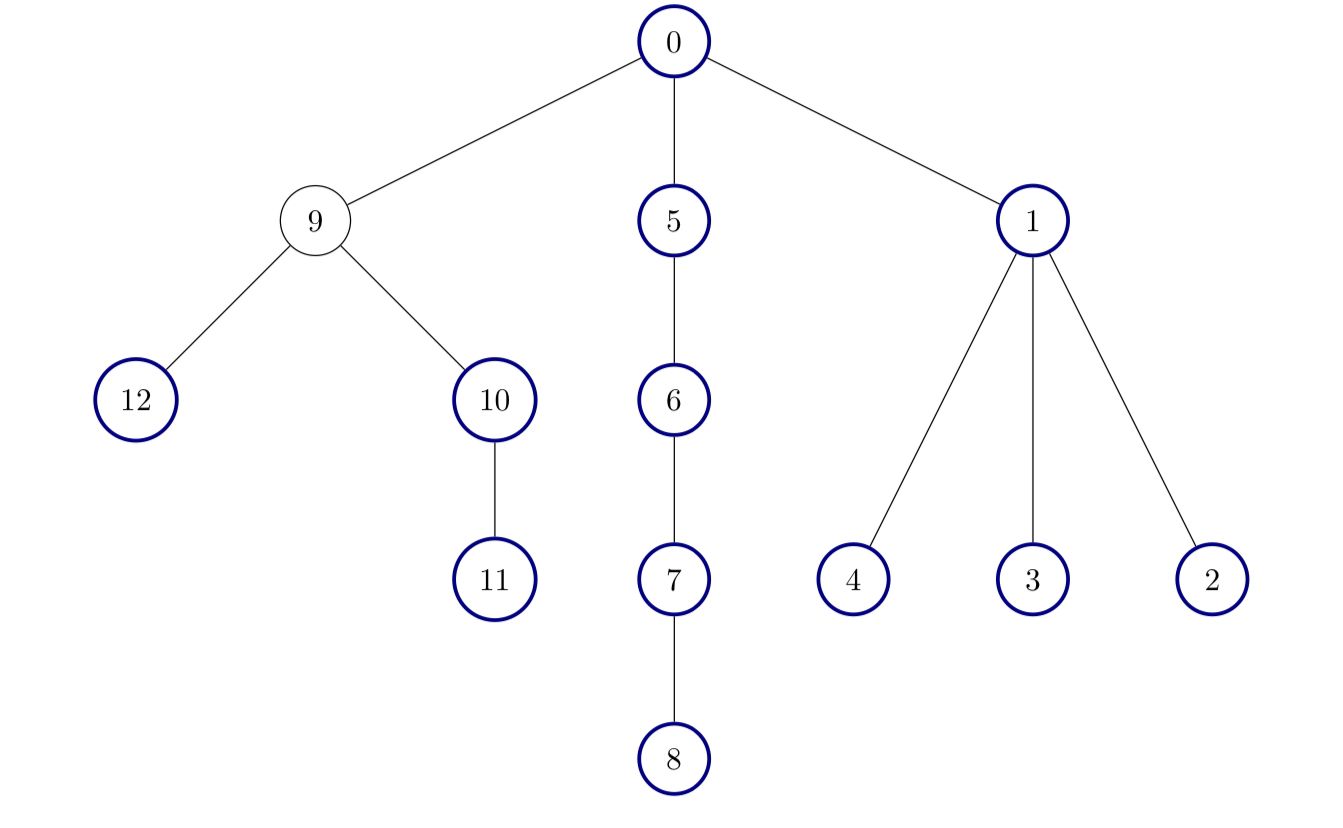
除了节点 9 以外其他所有节点都是好节点。
提示:
2 <= n <= 10^5edges.length == n - 1edges[i].length == 20 <= ai, bi < n- 输入确保
edges总表示一棵有效的树。
思路
建树操作可以参考本题,使用 unordered_map 创建无向树(有向树和无向树的区别在于向 unordered_map 中 push 的内容)。
dfs 时要注意不要回溯到父节点。这里利用 unordered_set 不允许重复元素的特性,判断当前节点的所有子节点为根的子树包含的节点数是否相等。
class Solution {
private:
unordered_map<int, vector<int>> tree;
int goodNodes;
public:
int dfs(int node, int parent) {
int size = 1; // 自身也算在子树节点数目中
unordered_set<int> childSizes;
for (auto child: tree[node]) {
if (child != parent) {
int childSubtreeSize = dfs(child, node);
size += childSubtreeSize;
childSizes.insert(childSubtreeSize);
}
}
if (childSizes.size() <= 1) {
goodNodes++;
}
return size;
}
int countGoodNodes(vector<vector<int>>& edges) {
int n = edges.size() + 1;
goodNodes = 0;
tree.clear();
for (const auto& edge: edges) {
tree[edge[0]].push_back(edge[1]);
tree[edge[1]].push_back(edge[0]);
}
dfs(0, -1);
return goodNodes;
}
};
24.单调数组对的数目Ⅱ
给你一个长度为 n 的 正 整数数组 nums 。
如果两个 非负 整数数组 (arr1, arr2) 满足以下条件,我们称它们是 单调 数组对:
- 两个数组的长度都是
n。 arr1是单调 非递减 的,换句话说arr1[0] <= arr1[1] <= ... <= arr1[n - 1]。arr2是单调 非递增 的,换句话说arr2[0] >= arr2[1] >= ... >= arr2[n - 1]。- 对于所有的
0 <= i <= n - 1都有arr1[i] + arr2[i] == nums[i]。
请你返回所有 单调 数组对的数目。
由于答案可能很大,请你将它对 109 + 7 取余 后返回。
示例 1:
输入:nums = [2,3,2]
输出:4
解释:
单调数组对包括:
([0, 1, 1], [2, 2, 1])([0, 1, 2], [2, 2, 0])([0, 2, 2], [2, 1, 0])([1, 2, 2], [1, 1, 0])
示例 2:
输入:nums = [5,5,5,5]
输出:126
提示:
1 <= n == nums.length <= 20001 <= nums[i] <= 1000
思路
记 f(i, j) 表示考虑前 i 个元素,且 arr1[i] = j 的方案数。
由于 arr1[i] + arr2[i] == nums[i] ,因此 arr2[i] = nums[i] - arr1[i] = nums[i] - j 。
考虑 arr1[i-1] = j' ,根据题目要求:
arr1非递减,因此j' <= jarr2非递增,因此nums[i] - j <= nums[i-1] - j',移项得j' <= j + nums[i-1] - nums[i]
因此 f(i, j) = sum(f(i-1, j')) ,其中 j' <= min(j, j + nums[i-1] - nums[i]) ,可以使用前缀和优化。
class Solution {
public:
int countOfPairs(vector<int>& nums) {
int n = nums.size();
int mx = 0;
for (int x : nums) mx = max(mx, x);
const int MOD = 1e9 + 7;
// 初始化 f[0][j] 以及对应的前缀和
long long f[n][mx+1], g[n][mx+1];
memset(f, 0, sizeof(f)); memset(g, 0, sizeof(g));
for (int i = 0; i <= nums[0]; i++) f[0][i] = 1;
g[0][0] = f[0][0];
for (int i = 1; i <= mx; i++) g[0][i] = (g[0][i - 1] + f[0][i]) % MOD;
for (int i = 1; i < n; i++) {
// 计算单个 DP 状态
for (int j = 0; j <= nums[i]; j++) {
int lim = min(j, j + nums[i - 1] - nums[i]);
if (lim >= 0) f[i][j] = g[i - 1][lim];
}
// 计算前缀和
g[i][0] = f[i][0];
for (int j = 1; j <= mx; j++) g[i][j] = (g[i][j - 1] + f[i][j]) % MOD;
}
return g[n - 1][mx];
}
};
25.特殊数组Ⅱ(前缀和)
如果数组的每一对相邻元素都是两个奇偶性不同的数字,则该数组被认为是一个 特殊数组 。
你有一个整数数组 nums 和一个二维整数矩阵 queries,对于 queries[i] = [fromi, toi],请你帮助你检查
子数组 nums[fromi..toi] 是不是一个 特殊数组 。
返回布尔数组 answer,如果 nums[fromi..toi] 是特殊数组,则 answer[i] 为 true ,否则,answer[i] 为 false 。
示例 1:
输入:nums = [3,4,1,2,6], queries = [[0,4]]
输出:[false]
解释:
子数组是 [3,4,1,2,6]。2 和 6 都是偶数。
示例 2:
输入:nums = [4,3,1,6], queries = [[0,2],[2,3]]
输出:[false,true]
解释:
- 子数组是
[4,3,1]。3 和 1 都是奇数。因此这个查询的答案是false。 - 子数组是
[1,6]。只有一对:(1,6),且包含了奇偶性不同的数字。因此这个查询的答案是true。
提示:
1 <= nums.length <= 10^51 <= nums[i] <= 10^51 <= queries.length <= 10^5queries[i].length == 20 <= queries[i][0] <= queries[i][1] <= nums.length - 1
思路
如果直接对于每个询问去遍历 nums[from]到nums[to] ,是 O(n^2) 的复杂度,看数据范围一定会超时。
如果一个子数组存在一堆相邻元素,它们的奇偶性相同,那么这个子数组一定不是特殊数组。
怎么快速判断是否有奇偶性相同的相邻元素?
我们考虑这样一个问题:对于一个只含有 0 和 1 的数组,如何快速判断一个子数组是否全为 0 ?
如果子数组的元素和为 0 ,那么这个子数组一定全为 0 ;如果子数组的元素和大于 0 ,那么子数组一定包含 1 。
对于本题,定义一个长度为 n-1 的数组,a ,其中:
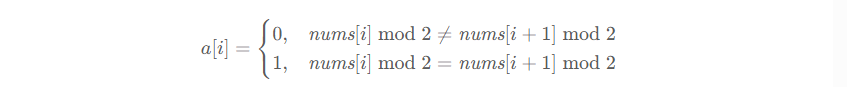
如果 a 的下标从 from 到 to-1 的子数组和等于 0 ,就说明 nums 的下标从 from 到 to 的这个子数组,其所有相邻元素的奇偶性都不同,那么该子数组就为特殊数组。
计算 a 的前缀和 s ,可以快速判断子数组和是否为 0 ,也就是判断:s[to] - s[from] = 0 ,即:s[from] = s[to]
代码如下:
class Solution {
public:
vector<bool> isArraySpecial(vector<int>& nums, vector<vector<int>>& queries) {
vector<int> s(nums.size());
for (int i = 1; i < nums.size(); ++i) {
s[i] = s[i-1] + (nums[i-1] % 2 == nums[i] % 2);
}
vector<bool> res(queries.size());
for (int i = 0; i < queries.size(); ++i) {
auto& q = queries[i];
res[i] = s[q[0]] == s[q[1]];
}
return res;
}
};
26.最高乘法得分
给你一个大小为 4 的整数数组 a 和一个大小 至少为 4 的整数数组 b。
你需要从数组 b 中选择四个下标 i0, i1, i2, 和 i3,并满足 i0 < i1 < i2 < i3。你的得分将是 a[0] * b[i0] + a[1] * b[i1] + a[2] * b[i2] + a[3] * b[i3] 的值。
返回你能够获得的 最大 得分。
示例 1:
输入: a = [3,2,5,6], b = [2,-6,4,-5,-3,2,-7]
输出: 26
解释:
选择下标 0, 1, 2 和 5。得分为 3 * 2 + 2 * (-6) + 5 * 4 + 6 * 2 = 26。
示例 2:
输入: a = [-1,4,5,-2], b = [-5,-1,-3,-2,-4]
输出: -1
解释:
选择下标 0, 1, 3 和 4。得分为 (-1) * (-5) + 4 * (-1) + 5 * (-2) + (-2) * (-4) = -1。
提示:
a.length == 44 <= b.length <= 10^5-10^5 <= a[i], b[i] <= 10^5
思路
我们需要从数组 b 中选出一个长度为 4 的子序列,将其与数组 a 对应相乘,得到最大值。
从右往左思考,我们以a=[3,2,5,6], b=[2,−6,4,−5,−3,2,−7] 为例。
从数组 b 的最右边开始,考虑选或不选 b[6] :
- 选
b[6],那么问题就转换成从b[0]到b[5]选 3 个数,使得最后结果最大; - 不选
b[6],那么问题就转换成从b[0]到b[5]选 4 个数,使得最后结果最大;
考虑选或不选,可以将原问题转换成规模更小的相似的子问题。
我们定义:dp[i][j] 表示从 b[0] 到 b[i] 选 j + 1 个数得到的最大值,基于上面的分析,有:
- 不选
b[i],那么只需要考虑从b[0]到b[i-1]的最大值:dp[i][j] = dp[i-1][j]; - 选
b[i],那么需要考虑从b[0]到b[i-1]中选j个数得到的最大值:dp[i][j] = dp[i-1][j-1] + b[i] * a[j]
两者取最大值(表示选或不选):dp[i][j] = max(dp[i-1][j], dp[i-1][j-1] + b[i] * a[j])
class Solution {
public:
long long maxScore(vector<int>& a, vector<int>& b) {
int n = b.size();
vector<vector<long long>> dp(n + 1, vector<long long>(5));
for (int j = 1; j < 5; ++j) dp[0][j] = LLONG_MIN / 2;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < 4; ++j) {
dp[i+1][j+1] = max(dp[i][j+1], dp[i][j] + (long long) a[j] * b[i]);
}
}
return dp[n][4];
}
};
27.坐上公交的最晚时间
链接:2332. 坐上公交的最晚时间 - 力扣(LeetCode)
给你一个下标从 0 开始长度为 n 的整数数组 buses ,其中 buses[i] 表示第 i 辆公交车的出发时间。同时给你一个下标从 0 开始长度为 m 的整数数组 passengers ,其中 passengers[j] 表示第 j 位乘客的到达时间。所有公交车出发的时间互不相同,所有乘客到达的时间也互不相同。
给你一个整数 capacity ,表示每辆公交车 最多 能容纳的乘客数目。
每位乘客都会搭乘下一辆有座位的公交车。如果你在 y 时刻到达,公交在 x 时刻出发,满足 y <= x 且公交没有满,那么你可以搭乘这一辆公交。最早 到达的乘客优先上车。
返回你可以搭乘公交车的最晚到达公交站时间。你 不能 跟别的乘客同时刻到达。
注意:数组 buses 和 passengers 不一定是有序的。
示例 1:
输入:buses = [10,20], passengers = [2,17,18,19], capacity = 2
输出:16
解释:
第 1 辆公交车载着第 1 位乘客。
第 2 辆公交车载着你和第 2 位乘客。
注意你不能跟其他乘客同一时间到达,所以你必须在第二位乘客之前到达。
示例 2:
输入:buses = [20,30,10], passengers = [19,13,26,4,25,11,21], capacity = 2
输出:20
解释:
第 1 辆公交车载着第 4 位乘客。
第 2 辆公交车载着第 6 位和第 2 位乘客。
第 3 辆公交车载着第 1 位乘客和你。
思路
要得到能坐上公交的最晚时间,可以从后往前思考。
由于原数组不一定有序,我们先对两个数组分别进行排序。
- 首先模拟当前所有乘客都上车的过程;
- 然后从后往前思考,从最后一辆车开始,寻找能插队的位置:
- 对于最后一辆车,假如所有乘客上车后仍然有空位,我们可以卡在最后一辆车发车的时间点上车;
- 如果没有空位,那么就往前找,看有哪个时间点是没有乘客上车的,我们在这个时间点上车,把后面的乘客挤下去(插队)
class Solution {
public:
int latestTimeCatchTheBus(vector<int>& buses, vector<int>& passengers, int capacity) {
ranges::sort(buses);
ranges::sort(passengers);
// 模拟上车
int j = 0, c;
for (auto t: buses) {
for (c = capacity; c && j < passengers.size() && passengers[j] <= t; --c) {
++j;
}
}
// 模拟插队
--j;
// 判断最后一辆车是否有空位
int ans = c ? buses.back() : passengers[j];
// 往前找插队的位置
while (j >= 0 && ans == passengers[j]) {
--ans;
--j;
}
return ans;
}
};
28.适龄的朋友(滑动窗口)
在社交媒体网站上有 n 个用户。给你一个整数数组 ages ,其中 ages[i] 是第 i 个用户的年龄。
如果下述任意一个条件为真,那么用户 x 将不会向用户 y(x != y)发送好友请求:
ages[y] <= 0.5 * ages[x] + 7ages[y] > ages[x]ages[y] > 100 && ages[x] < 100
否则,x 将会向 y 发送一条好友请求。
注意,如果 x 向 y 发送一条好友请求,y 不必也向 x 发送一条好友请求。另外,用户不会向自己发送好友请求。
返回在该社交媒体网站上产生的好友请求总数。
示例 1:
输入:ages = [16,16]
输出:2
解释:2 人互发好友请求。
示例 2:
输入:ages = [16,17,18]
输出:2
解释:产生的好友请求为 17 -> 16 ,18 -> 17 。
示例 3:
输入:ages = [20,30,100,110,120]
输出:3
解释:产生的好友请求为 110 -> 100 ,120 -> 110 ,120 -> 100 。
提示:
n == ages.length1 <= n <= 2 * 10^41 <= ages[i] <= 120
思路
将原有的三个条件改写,当同时满足下面的条件时, x 向 y 发送好友请求:
0.5 * ages[x] + 7 < ages[y] <= ages[x]x != y
注意到,如果第一个条件中的 ages[y] <= ages[x] 成立,那么题目中的第三个条件按必定不成立。
我们用一个长为 121 的 cnt 数组统计每个年龄的人数。
枚举年龄 ageX ,我们需要知道:
- 可以发送好友请求的最小年龄
ageY是多少 - 年龄在
[ageY, ageX]中的人数
由于 ageX 越大,ageY 也越大,可以考虑滑动窗口。我们维护 [ageY, ageX] 中的人数 cnt_window ,如果 cnt_window > 0 ,说明存在可以发送好友请求的用户:
- 当前
cnt[ageX]个用户可以与cnt_window个用户发送好友请求,那么总共有cnt[ageX] * cnt_window个请求 - 其中有
cnt[ageX]个好友请求是自己发给自己的,需要减去
所以将 cnt[ageX] * cnt_window - cnt[ageX] 加入答案
Code
class Solution {
public:
int numFriendRequests(vector<int>& ages) {
int res = 0;
int cnt[121]{};
for (int age: ages) cnt[age]++;
int age_y = 0, cnt_window = 0;
for (int age_x = 0; age_x < 121; ++age_x) {
cnt_window += cnt[age_x];
while (2 * age_y <= age_x + 14) {
cnt_window -= cnt[age_y];
++age_y;
}
if (cnt_window > 0) {
res += cnt_window * cnt[age_x] - cnt[age_x];
}
}
return res;
}
};
