前缀和

区域和检索 - 数组不可变

给定一个整数数组 nums，处理以下类型的多个查询:

1. 计算索引 left 和 right （包含 left 和 right）之间的 nums 元素的 和 ，其中 left <= right

实现 NumArray 类：

• NumArray(int[] nums) 使用数组 nums 初始化对象
• int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的 总和 ，包含 left 和 right 两点（也就是 nums[left] + nums[left + 1] + ... + nums[right] )

示例 1：

输入：
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出：
[null, 1, -1, -3]

解释：
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1)) 
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))

提示：

• 1 <= nums.length <= 10^4
• -10^5 <= nums[i] <= 10^5
• 0 <= i <= j < nums.length
• 最多调用 10^4 次 sumRange 方法

思路

为了方便描述，把 nums 记作 a 。

对于数组 a ，定义它的前缀和：

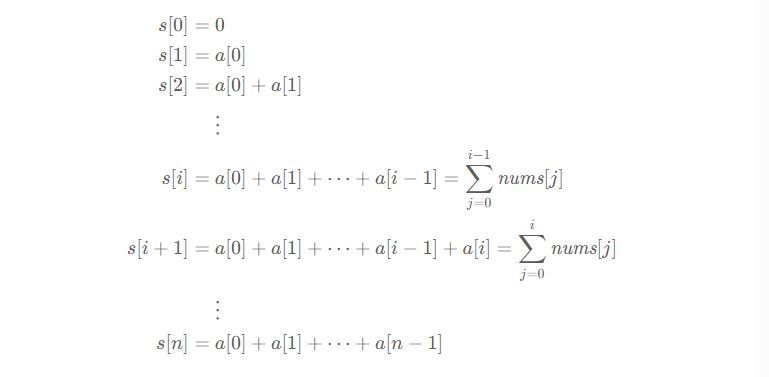
为什么要定义 s[0] = 0 ，见下文。

根据这个定义，有：s[i+1] = s[i] + a[i]

示例中的数组 [-2,0,3,-5,2,-1] 对应的前缀和数组 s = [0,-2,-2,1,-4,-2,-3] 。

通过前缀和，我们可以把连续子数组的元素和转换成两个前缀和的差，a[left] 到 a[right] 的元素和等于：

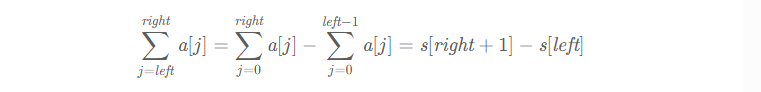
有了这个式子，示例中子数组 [3,-5,2,-1] 的和，就可以用 O(1) 的时间计算出来：s[6] - s[2] = -1

至于为什么要定义 s[0] = 0 ，这样做有什么好处？

如果 left = 0，要计算的子数组是一个前缀（从 a[0] 到 a[right]），我们要用 s[right+1] 减去 s[0]。如果不定义 s[0] = 0，就必须特判 left = 0 的情况了。通过定义 s[0] = 0，任意子数组（包括前缀）都可以表示为两个前缀和的差。此外，如果 a 是空数组，定义 s[0] = 0 的写法是可以兼容这种情况的。

Code

class NumArray {
private:
    vector<int> pre;

public:
    NumArray(vector<int>& nums) {
        int n = nums.size();
        // 维护一个前缀和
        pre.resize(n + 1);
        for (int i = 0; i < n; ++i) {
            pre[i+1] = pre[i] + nums[i];
        }
    }
    
    int sumRange(int left, int right) {
        return pre[right+1] - pre[left];
    }
};

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray* obj = new NumArray(nums);
 * int param_1 = obj->sumRange(left,right);
 */

例题

统计范围内的元音字符串数

给你一个下标从 0 开始的字符串数组 words 以及一个二维整数数组 queries 。

每个查询 queries[i] = [li, ri] 会要求我们统计在 words 中下标在 li 到 ri 范围内（包含 这两个值）并且以元音开头和结尾的字符串的数目。

返回一个整数数组，其中数组的第 i 个元素对应第 i 个查询的答案。

注意：元音字母是 'a'、'e'、'i'、'o' 和 'u' 。

示例 1：

输入：words = ["aba","bcb","ece","aa","e"], queries = [[0,2],[1,4],[1,1]]
输出：[2,3,0]
解释：以元音开头和结尾的字符串是 "aba"、"ece"、"aa" 和 "e" 。
查询 [0,2] 结果为 2（字符串 "aba" 和 "ece"）。
查询 [1,4] 结果为 3（字符串 "ece"、"aa"、"e"）。
查询 [1,1] 结果为 0 。
返回结果 [2,3,0] 。

示例 2：

输入：words = ["a","e","i"], queries = [[0,2],[0,1],[2,2]]
输出：[3,2,1]
解释：每个字符串都满足这一条件，所以返回 [3,2,1] 。

提示：

• 1 <= words.length <= 10^5
• 1 <= words[i].length <= 40
• words[i] 仅由小写英文字母组成
• sum(words[i].length) <= 3 * 10^5
• 1 <= queries.length <= 10^5
• 0 <= queries[j][0] <= queries[j][1] < words.length

思路

维护一个前缀和数组 pre ，用来记录 words 中前 i 个字符串里元音字符串的个数，其他思路和引入中的例题相同。

Code

class Solution {
public:
    unordered_set<char> letters = {'a', 'e', 'i', 'o', 'u'};

    vector<int> vowelStrings(vector<string>& words, vector<vector<int>>& queries) {
        int n = words.size();
        vector<int> pre(n + 1);
        for (int i = 0; i < n; ++i) {
            string word = words[i];
            int len = word.length();
            char a = word.at(0), b = word.at(len-1);
            if (letters.count(a) && letters.count(b)) {
                pre[i+1] = pre[i] + 1;
            } else {
                pre[i+1] = pre[i];
            }
        }

        vector<int> res;
        for (const auto& q: queries) {
            int left = q[0], right = q[1];
            res.push_back(pre[right+1] - pre[left]);
        }
        return res;
    }
};

特殊数组Ⅱ

如果数组的每一对相邻元素都是两个奇偶性不同的数字，则该数组被认为是一个 特殊数组 。

你有一个整数数组 nums 和一个二维整数矩阵 queries，对于 queries[i] = [fromi, toi]，请你帮助你检查子数组 nums[fromi..toi] 是不是一个 特殊数组 。

返回布尔数组 answer，如果 nums[fromi..toi] 是特殊数组，则 answer[i] 为 true ，否则，answer[i] 为 false 。

示例 1：

输入：nums = [3,4,1,2,6], queries = [[0,4]]

输出：[false]

解释：

子数组是 [3,4,1,2,6]。2 和 6 都是偶数。

示例 2：

输入：nums = [4,3,1,6], queries = [[0,2],[2,3]]

输出：[false,true]

解释：

1. 子数组是 [4,3,1]。3 和 1 都是奇数。因此这个查询的答案是 false。
2. 子数组是 [1,6]。只有一对：(1,6)，且包含了奇偶性不同的数字。因此这个查询的答案是 true。

提示：

• 1 <= nums.length <= 10^5
• 1 <= nums[i] <= 10^5
• 1 <= queries.length <= 10^5
• queries[i].length == 2
• 0 <= queries[i][0] <= queries[i][1] <= nums.length - 1

思路

如果直接对于每个询问去遍历 nums[from]到nums[to] ，是 O(n^2) 的复杂度，看数据范围一定会超时。

如果一个子数组存在一堆相邻元素，它们的奇偶性相同，那么这个子数组一定不是特殊数组。

怎么快速判断是否有奇偶性相同的相邻元素？

我们考虑这样一个问题：对于一个只含有 0 和 1 的数组，如何快速判断一个子数组是否全为 0 ？

如果子数组的元素和为 0 ，那么这个子数组一定全为 0 ；如果子数组的元素和大于 0 ，那么子数组一定包含 1 。

对于本题，定义一个长度为 n-1 的数组，a ，其中：

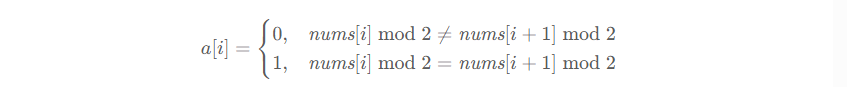
如果 a 的下标从 from 到 to-1 的子数组和等于 0 ，就说明 nums 的下标从 from 到 to 的这个子数组，其所有相邻元素的奇偶性都不同，那么该子数组就为特殊数组。

计算 a 的前缀和 s ，可以快速判断子数组和是否为 0 ，也就是判断：s[to] - s[from] = 0 ，即：s[from] = s[to]

Code：

class Solution {
public:
    vector<bool> isArraySpecial(vector<int>& nums, vector<vector<int>>& queries) {
        vector<int> s(nums.size());
        for (int i = 1; i < nums.size(); ++i) {
            s[i] = s[i-1] + (nums[i-1] % 2 == nums[i] % 2);
        }
        vector<bool> res(queries.size());
        for (int i = 0; i < queries.size(); ++i) {
            auto& q = queries[i];
            res[i] = s[q[0]] == s[q[1]];
        }
        return res;
    }
};

蜡烛之间的盘子

给你一个长桌子，桌子上盘子和蜡烛排成一列。给你一个下标从 0 开始的字符串 s ，它只包含字符 '*' 和 '|' ，其中 '*' 表示一个 盘子 ，'|' 表示一支 蜡烛 。

同时给你一个下标从 0 开始的二维整数数组 queries ，其中 queries[i] = [lefti, righti] 表示 子字符串 s[lefti...righti] （包含左右端点的字符）。对于每个查询，你需要找到 子字符串中 在 两支蜡烛之间 的盘子的 数目 。如果一个盘子在 子字符串中 左边和右边 都 至少有一支蜡烛，那么这个盘子满足在 两支蜡烛之间 。

• 比方说，s = "||**||**|*" ，查询 [3, 8] ，表示的是子字符串 "*||**|" 。子字符串中在两支蜡烛之间的盘子数目为 2 ，子字符串中右边两个盘子在它们左边和右边 都 至少有一支蜡烛。

请你返回一个整数数组 answer ，其中 answer[i] 是第 i 个查询的答案。

示例 1:

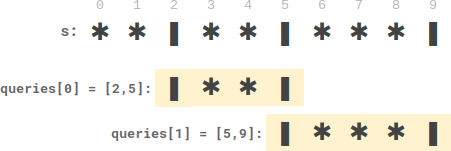
输入：s = "**|**|***|", queries = [[2,5],[5,9]]
输出：[2,3]
解释：
- queries[0] 有两个盘子在蜡烛之间。
- queries[1] 有三个盘子在蜡烛之间。

示例 2:

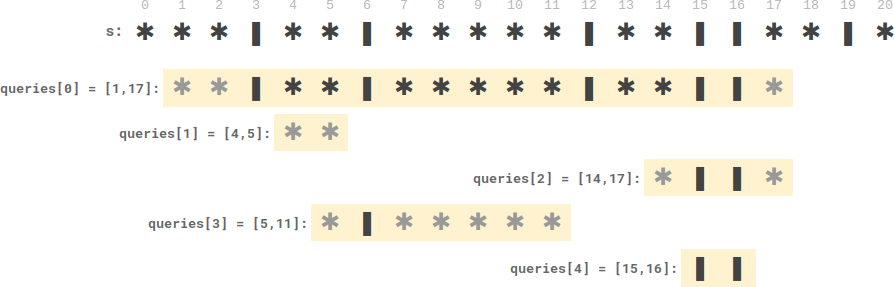
输入：s = "***|**|*****|**||**|*", queries = [[1,17],[4,5],[14,17],[5,11],[15,16]]
输出：[9,0,0,0,0]
解释：
- queries[0] 有 9 个盘子在蜡烛之间。
- 另一个查询没有盘子在蜡烛之间。

提示：

• 3 <= s.length <= 10^5
• s 只包含字符 '*' 和 '|' 。
• 1 <= queries.length <= 10^5
• queries[i].length == 2
• 0 <= lefti <= righti < s.length

思路

对于每一个询问，我们只需要找到给定区间内最左侧和最右侧的两个蜡烛，这样两个蜡烛之间的所有盘子都是符合条件的。

我们记录以每个位置结尾的累计盘子数量作为前缀和；

对于每个位置，记录从它开始往左数，遇到的第一个蜡烛（可以自身是蜡烛）；从他开始往右数，遇到的第一个蜡烛（可以自身是蜡烛）；

于是，对于每一个询问 q ，我们找到给定区间最左侧和最右侧两个位置，分别记为 q[0] 和 q[1] ，那么从 q[0] 开始往右数遇到的第一个蜡烛就是给定区间最左侧的蜡烛，从 q[1] 开始往左数遇到的第一个蜡烛就是给定区间最右侧的蜡烛。

最后返回这两个蜡烛之间的盘子数目即可，具体可通过前面计算的前缀和得到。

注意还需要判断当前位置左右不存在蜡烛的情况，此处用 -1 来特判。

Code：

class Solution {
public:
    vector<int> platesBetweenCandles(string s, vector<vector<int>>& queries) {
        int n = s.length();
        // 计算盘子数量前缀和
        vector<int> preSum(n);
        for (int i = 0, sum = 0; i < n; ++i) {
            if (s[i] == '*') {
                ++sum;
            }
            preSum[i] = sum;
        }

        // 预处理每个位置左侧的第一个蜡烛
        vector<int> left(n);
        for (int i = 0, l = -1; i < n; ++i) {
            if (s[i] == '|') {
                l = i;
            }
            left[i] = l;
        }

        // 预处理每个位置右侧的第一个蜡烛
        vector<int> right(n);
        for (int i = n - 1, r = -1; i >= 0; --i) {
            if (s[i] == '|') {
                r = i;
            }
            right[i] = r;
        }

        vector<int> ans;
        for (auto& q: queries) {
            int x = right[q[0]], y = left[q[1]];
            // x == -1 和 y == -1 表示当前位置左右不存在蜡烛的情况
            ans.push_back(x == -1 || y == -1 || x >= y ? 0 : preSum[y] - preSum[x]);
        }
        return ans;
    }
};

你能在你喜欢的那天吃到你喜欢的糖果吗？

给你一个下标从 0 开始的正整数数组 candiesCount ，其中 candiesCount[i] 表示你拥有的第 i 类糖果的数目。同时给你一个二维数组 queries ，其中 queries[i] = [favoriteTypei, favoriteDayi, dailyCapi] 。

你按照如下规则进行一场游戏：

• 你从第 **0** 天开始吃糖果。
• 你在吃完 所有 第 i - 1 类糖果之前，不能 吃任何一颗第 i 类糖果。
• 在吃完所有糖果之前，你必须每天 至少 吃 一颗 糖果。

请你构建一个布尔型数组 answer ，用以给出 queries 中每一项的对应答案。此数组满足：

• answer.length == queries.length 。answer[i] 是 queries[i] 的答案。
• answer[i] 为 true 的条件是：在每天吃 不超过 dailyCapi 颗糖果的前提下，你可以在第 favoriteDayi 天吃到第 favoriteTypei 类糖果；否则 answer[i] 为 false 。

注意，只要满足上面 3 条规则中的第二条规则，你就可以在同一天吃不同类型的糖果。

请你返回得到的数组 answer 。

示例 1：

输入：candiesCount = [7,4,5,3,8], queries = [[0,2,2],[4,2,4],[2,13,1000000000]]
输出：[true,false,true]
提示：
1- 在第 0 天吃 2 颗糖果(类型 0），第 1 天吃 2 颗糖果（类型 0），第 2 天你可以吃到类型 0 的糖果。
2- 每天你最多吃 4 颗糖果。即使第 0 天吃 4 颗糖果（类型 0），第 1 天吃 4 颗糖果（类型 0 和类型 1），你也没办法在第 2 天吃到类型 4 的糖果。换言之，你没法在每天吃 4 颗糖果的限制下在第 2 天吃到第 4 类糖果。
3- 如果你每天吃 1 颗糖果，你可以在第 13 天吃到类型 2 的糖果。

示例 2：

输入：candiesCount = [5,2,6,4,1], queries = [[3,1,2],[4,10,3],[3,10,100],[4,100,30],[1,3,1]]
输出：[false,true,true,false,false]

提示：

• 1 <= candiesCount.length <= 10^5
• 1 <= candiesCount[i] <= 10^5
• 1 <= queries.length <= 10^5
• queries[i].length == 3
• 0 <= favoriteTypei < candiesCount.length
• 0 <= favoriteDayi <= 10^9
• 1 <= dailyCapi <= 10^9

思路

题目有点长，读懂了其实就是个前缀和

由于吃糖果必须按照从前到后的顺序，所以用前缀和记录吃完第 i 种糖果后总共吃掉了多少糖果，

将其记为 pre[i] ，那么有： pre[i] = pre[i-1] + candiesCount[i] 。

对于每个询问 q ，记 q[0] 为 type 、q[1] 为 day 、q[2] 为 cap ，

分别计算按照最大速度 cap 吃糖果共需要的天数，得到最早能吃到第 type 种糖果的日期，

和按照最低速度 1 吃糖果共需要的天数，得到最晚吃到第 type 种糖果的日期。

判断 day 是否在这个范围内即可。

Code：

class Solution {
public:
    vector<bool> canEat(vector<int>& candiesCount, vector<vector<int>>& queries) {
        int n = candiesCount.size();
        vector<long long> pre(n); // 要吃完第 i 种糖果，至少要吃 pre[i] 个糖果
        pre[0] = candiesCount[0];
        for (int i = 1; i < n; ++i) {
            pre[i] = pre[i-1] + candiesCount[i];
        }

        vector<bool> res;
        for (const auto& q: queries) {
            long long type = q[0], day = q[1], cap = q[2];
            long long x1 = day + 1;
            long long y1 = (long long) (day + 1) * cap;
            long long x2 = (type == 0 ? 1 : pre[type-1] + 1);
            long long y2 = pre[type];
            res.push_back(!(x1 > y2 || y1 < x2));
        }
        return res;
    }
};

差分数组

考虑数组 a=[1,3,3,5,8]，对其中的相邻元素两两作差（右边减左边），得到数组 [2,0,2,3]。然后在开头补上 a[0]，得到差分数组：d = [1,2,0,2,3] 。

这有什么用呢？如果从左到右累加 d 中的元素，我们就「还原」回了 a 数组 [1,3,3,5,8]。这类似求导与积分的概念。

这又有什么用呢？现在把连续子数组 a[1],a[2],a[3] 都加上 10，得到 a′=[1,13,13,15,8]。再次两两作差，并在开头补上 a′[0]，得到差分数组：d'=[1,12,0,2,−7]

对比 d 和 d′，可以发现只有 d[1] 和 d[4] 变化了，这意味着对 a 中连续子数组的操作，可以转变成对差分数组 d 中两个数的操作。

定义与性质：

对于数组 a，定义其差分数组（difference array）为

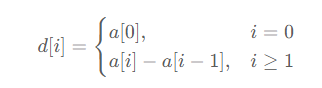
• 性质 1：从左到右累加 d 中的元素，可以得到数组 a

• 性质 2：如下两个操作是等价的。

  • 把 a 的子数组 a[i],a[i+1], ... ,a[j] 都加上 x 。
  • 把 d[i] 增加 x ，把 d[j+1] 减少 x 。

利用性质 2，我们只需要 O(1) 的时间就可以完成对 a 的子数组的操作。最后利用性质 1从差分数组复原出数组 a 。

例题

拼车

车上最初有 capacity 个空座位。车 只能 向一个方向行驶（也就是说，不允许掉头或改变方向）

给定整数 capacity 和一个数组 trips , trip[i] = [numPassengersi, fromi, toi] 表示第 i 次旅行有 numPassengersi 乘客，接他们和放他们的位置分别是 fromi 和 toi 。这些位置是从汽车的初始位置向东的公里数。

当且仅当你可以在所有给定的行程中接送所有乘客时，返回 true，否则请返回 false。

示例 1：

输入：trips = [[2,1,5],[3,3,7]], capacity = 4
输出：false

示例 2：

输入：trips = [[2,1,5],[3,3,7]], capacity = 5
输出：true

提示：

• 1 <= trips.length <= 1000
• trips[i].length == 3
• 1 <= numPassengersi <= 100
• 0 <= fromi < toi <= 1000
• 1 <= capacity <= 10^5

思路

不用差分数组时，可以开一个新数组 f ，f[i] 存放第 i 天车上的人数，然后遍历每个 trip ，将 f 的第 from 到 to - 1 都累加上 trip 中对应的人数（因为第 to 天时，当前 trip 的人都下车了，所以不用累加到第 to 天）。

计算完后直接比较 f 的最大值和 capacity 的大小即可。也可以在计算时发现 f 比 capacity 更大而直接返回

Code

class Solution {
public:
    bool carPooling(vector<vector<int>>& trips, int capacity) {
        int n = trips.size();
        vector<int> f(1005);
        for (int i = 0; i < n; ++i) {
            int num = trips[i][0], from = trips[i][1], to = trips[i][2];
            for (int j = from; j < to; ++j) {
                f[j] += num;
            }
        }
        if (*max_element(f.begin(), f.end()) > capacity) return false;
        return true;
    }
};

看了上面比较直接的思路，可以发现本题是处理给定数组区间的问题，我们要做的是将数组 f 的某一段区间加上 num ，这正好可以采用差分数组进行优化。

开一个对应大小的差分数组 d ，对于每个询问，我们只需要计算差分数组的头尾。

之后我们遍历差分数组进行累加，还原出原数组，判断有没有元素大于 capacity 即可。

class Solution {
public:
    bool carPooling(vector<vector<int>>& trips, int capacity) {
        int d[1001]{};
        for (auto& t: trips) {
            int num = t[0], from = t[1], to = t[2];
            d[from] += num;
            d[to] -= num;
        }
        int s = 0;
        for (auto v: d) {
            s += v;
            if (s > capacity) return false;
        }
        return true;
    }
};