交易逆序对的总数
在股票交易中,如果前一天的股价高于后一天的股价,则可以认为存在一个「交易逆序对」。请设计一个程序,输入一段时间内的股票交易记录 record,返回其中存在的「交易逆序对」总数。
示例 1:
输入:record = [9, 7, 5, 4, 6]
输出:8
解释:交易中的逆序对为 (9, 7), (9, 5), (9, 4), (9, 6), (7, 5), (7, 4), (7, 6), (5, 4)。
限制:
0 <= record.length <= 50000
Code
class Solution {
public:
int mergeSort(vector<int>& record, vector<int>& tmp, int l, int r) {
if (l >= r) return 0;
int mid = (l + r) / 2;
int inv_cnt = mergeSort(record, tmp, l, mid) + mergeSort(record, tmp, mid + 1, r);
int i = l, j = mid + 1, pos = l;
while (i <= mid && j <= r) {
if (record[i] <= record[j]) {
tmp[pos] = record[i];
++i;
inv_cnt += (j - (mid + 1));
} else {
tmp[pos] = record[j];
++j;
}
++pos;
}
for (int k = i; k <= mid; ++k) {
// 右边已经没有比左边当前数更大的了,直接加上 (j - (mid + 1))
tmp[pos++] = record[k];
inv_cnt += (j - (mid + 1));
}
for (int k = j; k <= r; ++k) {
tmp[pos++] = record[k];
}
copy(tmp.begin() + l, tmp.begin() + r + 1, record.begin() + l);
return inv_cnt;
}
int reversePairs(vector<int>& record) {
int n = record.size();
vector<int> tmp(n);
return mergeSort(record, tmp, 0, n - 1);
}
};
二分查找(闭区间写法)
int lower_bound(vector<int> &nums, int target) {
int left = 0, right = (int) nums.size() - 1; // 闭区间 [left, right]
while (left <= right) { // 区间不为空
// 循环不变量:
// nums[left-1] < target
// nums[right+1] >= target
// mid 也可以写成:int mid = ((right - left) >> 1) + left;
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1; // 范围缩小到 [mid+1, right]
} else {
right = mid - 1; // 范围缩小到 [left, mid-1]
}
}
return left;
}
如果要查找的数字不在数组中,上述写法会返回该数组中第一个大于 target 的数的下标。
比如:[1,4,7,11,15],查找 5 ,会返回 7 的下标,即:left = 2
另外:
- 如果传入的数字大于数组中最大的数,会返回
nums.size() - 如果传入的数字小于数组中最小的数,会返回 0
统计目标成绩的出现次数
某班级考试成绩按非严格递增顺序记录于整数数组 scores,请返回目标成绩 target 的出现次数。
示例 1:
输入: scores = [2, 2, 3, 4, 4, 4, 5, 6, 6, 8], target = 4
输出: 3
示例 2:
输入: scores = [1, 2, 3, 5, 7, 9], target = 6
输出: 0
提示:
0 <= scores.length <= 10^5-10^9 <= scores[i] <= 10^9scores是一个非递减数组-10^9 <= target <= 10^9
Code
class Solution {
public:
int lower_bound(vector<int>& nums, int target) {
int n = nums.size();
int left = 0, right = n - 1;
while (left <= right) {
int mid = ((right - left) >> 1) + left;
if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return left;
}
int countTarget(vector<int>& scores, int target) {
int start = lower_bound(scores, target);
int end = lower_bound(scores, target + 1);
return end - start;
}
};
完成旅途的最少时间
给你一个数组 time ,其中 time[i] 表示第 i 辆公交车完成 一趟旅途 所需要花费的时间。
每辆公交车可以 连续 完成多趟旅途,也就是说,一辆公交车当前旅途完成后,可以 立马开始 下一趟旅途。每辆公交车 独立 运行,也就是说可以同时有多辆公交车在运行且互不影响。
给你一个整数 totalTrips ,表示所有公交车 总共 需要完成的旅途数目。请你返回完成 至少 totalTrips 趟旅途需要花费的 最少 时间。
示例 1:
输入:time = [1,2,3], totalTrips = 5
输出:3
解释:
- 时刻 t = 1 ,每辆公交车完成的旅途数分别为 [1,0,0] 。
已完成的总旅途数为 1 + 0 + 0 = 1 。
- 时刻 t = 2 ,每辆公交车完成的旅途数分别为 [2,1,0] 。
已完成的总旅途数为 2 + 1 + 0 = 3 。
- 时刻 t = 3 ,每辆公交车完成的旅途数分别为 [3,1,1] 。
已完成的总旅途数为 3 + 1 + 1 = 5 。
所以总共完成至少 5 趟旅途的最少时间为 3 。
示例 2:
输入:time = [2], totalTrips = 1
输出:2
解释:
只有一辆公交车,它将在时刻 t = 2 完成第一趟旅途。
所以完成 1 趟旅途的最少时间为 2 。
提示:
1 <= time.length <= 10^51 <= time[i], totalTrips <= 10^7
思路
时间越多,可以完成的旅途也就越多,有单调性,可以二分答案。
问题变成:
- 每辆车都用时 x ,总共能完成多少趟旅途?能否达到 totalTrips ?
根据题意,我们可以完成
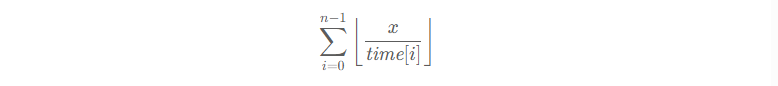
躺旅途,将它与 totalTrips 比较,如果比 totalTrips 小,说明二分答案小了,更新二分区间左端点 left ,否则更新二分区间右端点 right。
关于左右端点的初始化:
- 获取 time 数组的最小值 min_t,初始化 left 为 min_t - 1 ,在这个时间任何车都没法完成一趟旅途。
- 让最快的车完成 totalTrips 躺旅途,用时
min(time) * totalTrips,这个时间一定满足题目要求,初始化 right 为这个值。
Code
class Solution {
public:
long long minimumTime(vector<int>& time, int totalTrips) {
auto check = [&](long long x) -> bool {
long long sum = 0;
for (auto t: time) {
sum += x / t;
if (sum >= totalTrips) {
return true;
}
}
return false;
};
long long min_t = ranges::min(time);
long long left = min_t - 1;
long long right = min_t * totalTrips;
while (left <= right) {
long long mid = ((right - left) >> 1) + left;
if (check(mid)) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return left;
}
};
